题目内容
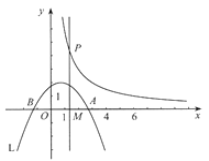
【题目】如图,抛物线L: ![]() (常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线
(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线![]() 于点P,且OA·MP=12.
于点P,且OA·MP=12.
(1)求k值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x0,且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
【答案】(1)6;(2)![]() ;(3)当t-2≤
;(3)当t-2≤![]() ,即t≤4时,顶点(t-2,2)就是G的最高点;当t>4时,L与MP的交点(
,即t≤4时,顶点(t-2,2)就是G的最高点;当t>4时,L与MP的交点(![]() )就是G的最高点.(4)
)就是G的最高点.(4)![]() .
.
【解析】
试题分析:(1)设设点P(x,y),则MP=y,由OA的中点为M知OA=2x,代入OA·MP=12,即可得xy=6,即k=6;(2)当t=1时,令y=0,0=![]() ,解得
,解得![]() .即可得AB=4,求得抛物线的对称轴,根据点M的坐标即可得直线MP与L对称轴之间的距离;(3)由抛物线的解析式可得A(t,0),B(t-4,0),即可得抛物线的对称轴为x=t-2,又因MP为直线x=
.即可得AB=4,求得抛物线的对称轴,根据点M的坐标即可得直线MP与L对称轴之间的距离;(3)由抛物线的解析式可得A(t,0),B(t-4,0),即可得抛物线的对称轴为x=t-2,又因MP为直线x=![]() ,当t-2≤
,当t-2≤![]() ,即t≤4时,顶点(t-2,2)就是G的最高点;当t>4时,L与MP的交点(
,即t≤4时,顶点(t-2,2)就是G的最高点;当t>4时,L与MP的交点(![]() )就是G的最高点.(4)对双曲线,当4≤x0≤6时,1≤y≤
)就是G的最高点.(4)对双曲线,当4≤x0≤6时,1≤y≤![]() ,即L与双曲线C(4,
,即L与双曲线C(4,![]() ),D(6,1)之间的一段有个交点.①由
),D(6,1)之间的一段有个交点.①由![]() =
=![]() ,解得
,解得![]() ;②由1=
;②由1=![]() ,解得
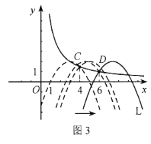
,解得![]() ;随着t的逐渐增大,L的位置随着点A(t,0)向右平移,如图3所示.当t=5时,L右侧过点C;当
;随着t的逐渐增大,L的位置随着点A(t,0)向右平移,如图3所示.当t=5时,L右侧过点C;当![]() 时,L右侧过点D;即
时,L右侧过点D;即![]() .当
.当![]() 时,L右侧离开了点D,而左侧未到点C,即L与该段无交点,舍去.当t=7时,L左侧过点C;当
时,L右侧离开了点D,而左侧未到点C,即L与该段无交点,舍去.当t=7时,L左侧过点C;当![]() 时,L左侧过点D;即
时,L左侧过点D;即![]() .
.
试题解析:(1)设点P(x,y),则MP=y,
由OA的中点为M知OA=2x,代入OA·MP=12,
得![]() ,即xy=6,
,即xy=6,
∴k=xy=6.
(2)当t=1时,令y=0,0=![]() ,∴
,∴![]() .
.
∴由B在A的左边,得B(-3,0),A(1,0),∴AB=4.
∵L的对称轴为x=-1,而M(![]() ,0),
,0),
∴MP与L对称轴的距离为![]() .
.
(3)∵A(t,0),B(t-4,0),
∴L的对称轴为x=t-2,
又MP为x=![]() ,
,
当t-2≤![]() ,即t≤4时,顶点(t-2,2)就是G的最高点;
,即t≤4时,顶点(t-2,2)就是G的最高点;
当t>4时,L与MP的交点(![]() )就是G的最高点.
)就是G的最高点.
(4)![]() .
.

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案