题目内容
供电局的电力维修工甲、乙两人要到45千米远的A地进行电力抢修.甲骑摩托车先行,t(t≥0)小时后乙开抢修车载着所需材料出发.(1)若t=
 (小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;
(小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;(2)若摩托车的速度是45千米/小时,抢修车的速度是60千米/小时,且乙不能比甲晚到则t的最大值是多少?
【答案】分析:(1)求的速度,路程明显,一定是根据时间来列等量关系,本题的关键描述语是:甲、乙两人同时到达.等量关系为:摩托车所用的时间-抢修车所用的时间= ;
;
(2)关系式为:抢修车所用的时间+t≤摩托车所用的时间.
解答:解:
(1)设摩托车的速度是x千米/时,则抢修车的速度是1.5x千米/时,
由题意得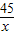 -
-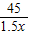 =
= ,(2分)
,(2分)
解之得x=40.(3分)
经检验,x=40千米/时是原方程的解且符合题意.
答:摩托车的速度为40千米/时.(4分)
(2)由题意得t+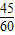 ≤
≤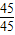 ,(6分)
,(6分)
解之得t≤ .
.
∴0≤t≤ .(7分)
.(7分)
∴t最大值是 (时)
(时)
答:乙最多只能比甲迟 小时出发.(8分)
小时出发.(8分)
点评:本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.本题用到的等量关系是:路程=速度×时间.
 ;
;(2)关系式为:抢修车所用的时间+t≤摩托车所用的时间.
解答:解:
(1)设摩托车的速度是x千米/时,则抢修车的速度是1.5x千米/时,
由题意得
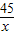 -
-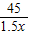 =
= ,(2分)
,(2分)解之得x=40.(3分)
经检验,x=40千米/时是原方程的解且符合题意.
答:摩托车的速度为40千米/时.(4分)
(2)由题意得t+
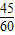 ≤
≤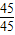 ,(6分)
,(6分)解之得t≤
 .
.∴0≤t≤
 .(7分)
.(7分)∴t最大值是
 (时)
(时)答:乙最多只能比甲迟
 小时出发.(8分)
小时出发.(8分)点评:本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.本题用到的等量关系是:路程=速度×时间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
供电局的电力维修工甲、乙两人要到30千米远的A地进行电力抢修.甲骑摩托车先行,
小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,求摩托车的速度.
(1)设摩托车的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.
(要求:填上适当的代数式,完成表格)
(2)列出方程,并求摩托车的速度.
| 1 |
| 4 |
(1)设摩托车的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.
(要求:填上适当的代数式,完成表格)
| 速度(千米/时) | 所走的路程(千米) | 所用时间(时) | |
| 摩托车 | x | 30 | |
| 抢修车 | 30 |
 是多少?
是多少?