题目内容
(2012•沙湾区模拟)甲:某供电局的电力维修工甲、乙两人要到45千米远的A地进行电力抢修.甲骑摩托车先行t(t≥0)小时后,乙开抢修车载着所需材料出发.
(1)若t=
小时,抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;
(2)若摩托车的速度是45千米/小时,抢修车的速度是60千米/小时,且乙不能比甲晚到,则t的最大值 是多少?
是多少?
乙:如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.若∠BAC=30°,EF⊥AB,垂足为F,连接DF.
求证:(1)△ABC≌△EAF;
(2)四边形ADFE是平行四边形.
(1)若t=
| 3 | 8 |
(2)若摩托车的速度是45千米/小时,抢修车的速度是60千米/小时,且乙不能比甲晚到,则t的最大值
 是多少?
是多少?乙:如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.若∠BAC=30°,EF⊥AB,垂足为F,连接DF.
求证:(1)△ABC≌△EAF;
(2)四边形ADFE是平行四边形.
分析:甲:(1)求的速度,路程明显,一定是根据时间来列等量关系,本题的关键描述语是:甲、乙两人同时到达.等量关系为:摩托车所用的时间-抢修车所用的时间=
;
(2)关系式为:抢修车所用的时间+t≤摩托车所用的时间.
乙:(1)首先Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后即可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF;
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
| 3 |
| 8 |
(2)关系式为:抢修车所用的时间+t≤摩托车所用的时间.
乙:(1)首先Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后即可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF;
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
解答:甲:解:(1)设摩托车的速度是x千米/时,则抢修车的速度是1.5x千米/时,
由题意得:
=
+
,
解之得x=40.
经检验,x=40千米/时是原方程的解且符合题意.
答:摩托车的速度为40千米/时.
(2)由题意得
≥t+
,
解之得t≤
.
∴0≤t≤
.
∴t最大值是
(时)
答:乙最多只能比甲迟
小时出发,即t的最大值为
.
乙:证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,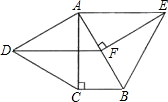
∴∠AEF=30°
∴AE=2AF,且AB=2AF,
∴AF=CB,
而∠ACB=∠AFE=90°,
在Rt△AFE和Rt△BCA中,
,
∴△ABC≌△EAF(HL);
(2)∵△AFE≌△BCA,
∴AC=EF,
而△ACD是等边三角形,
∴∠DAC=60°
∴EF=AC=AD,且AD⊥AB,
而EF⊥AB,
∴EF∥AD,
∴四边形ADFE是平行四边形.
由题意得:
| 45 |
| x |
| 45 |
| 1.5x |
| 3 |
| 8 |
解之得x=40.
经检验,x=40千米/时是原方程的解且符合题意.
答:摩托车的速度为40千米/时.
(2)由题意得
| 45 |
| 45 |
| 45 |
| 60 |
解之得t≤
| 1 |
| 4 |
∴0≤t≤
| 1 |
| 4 |
∴t最大值是
| 1 |
| 4 |
答:乙最多只能比甲迟
| 1 |
| 4 |
| 1 |
| 4 |
乙:证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,

∴∠AEF=30°
∴AE=2AF,且AB=2AF,
∴AF=CB,
而∠ACB=∠AFE=90°,
在Rt△AFE和Rt△BCA中,
|
∴△ABC≌△EAF(HL);
(2)∵△AFE≌△BCA,
∴AC=EF,
而△ACD是等边三角形,
∴∠DAC=60°
∴EF=AC=AD,且AD⊥AB,
而EF⊥AB,
∴EF∥AD,
∴四边形ADFE是平行四边形.
点评:本题考查了分式方程的应用以及利用等边三角形的性质证明全等三角形,然后利用全等三角形的性质和等边三角形的性质证明平行四边形,本题用到的等量关系是:路程=速度×时间.

练习册系列答案
相关题目
 B表示的数为m.
B表示的数为m. C(x2,0),且x2-x1=5.
C(x2,0),且x2-x1=5.