题目内容
已知整数a、b、c满足不等式a2+b2+c2+43≤ab+9b+8c,则a、b、c分别等于 .
a=3,b=6,c=4
试题分析:由已知条件构造完全平方公式,得(a﹣
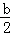 )2+3(
)2+3(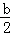 ﹣3)2+(c﹣4)2≤0,然后由非负数的性质求解.
﹣3)2+(c﹣4)2≤0,然后由非负数的性质求解.解:由已知得a2+b2+c2+43﹣ab﹣9b﹣8c≤0,
配方得(a﹣
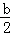 )2+3(
)2+3(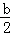 ﹣3)2+(c﹣4)2≤0,
﹣3)2+(c﹣4)2≤0,又∵(a﹣
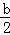 )2+3(
)2+3(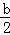 ﹣3)2+(c﹣4)2≥0,
﹣3)2+(c﹣4)2≥0,∴(a﹣
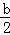 )2+3(
)2+3(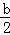 ﹣3)2+(c﹣4)2=0,
﹣3)2+(c﹣4)2=0,∴a﹣
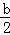 =0,
=0,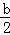 ﹣3=0,c﹣4=0,
﹣3=0,c﹣4=0,∴a=3,b=6,c=4.
故答案为:a=3,b=6,c=4.
点评:此题考查用分组分解法进行因式分解.难点是配方成非负数的形式,再根据非负数的性质求解.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
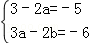 ,解得
,解得