题目内容
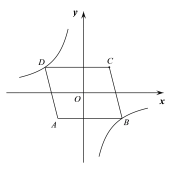
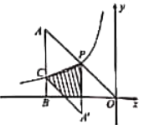
【题目】如图点P为双曲线
上一动点.连接OP并延长到点A，使
，过点A作x轴的垂线，垂足为B，交双曲线于点C.当
时，连接PC，将
沿直线PC进行翻折，则翻折后的
与四边形BOPC的重叠部分（图中阴影部分）的面积是_______________
【答案】
【解析】
设
交OB于E，
交OE于F，
，由题可知：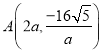
，
，在根据勾股定理即可求出a的值，从而求出
，
，C
，
，由折叠的性质和平行线的性质可得：
、
为直角三角形，并与
相似，从而求出BC、BF，利用三角形的面积公式，分别计算出△ABO、△BCF、△OEP和△APC的面积，从而求出阴影部分的面积.
解：设交OB于E，交OE于F
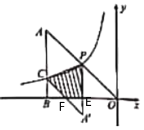
设，
∵
∴，
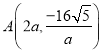又∵
即
，
∴
可得出
则，，C，
由折叠性质
又∵
∴
∴
同理
∴、为直角三角形，并与相似
∴
由
，故
，
，
∴
故答案为：.
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
