Question

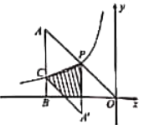
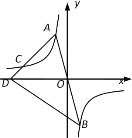
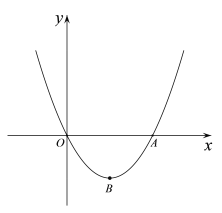
【题目】如图，抛物线y=x2+mx（m<0）交x轴于O，A两点，顶点为点B．

（1）求△AOB的面积（用含m的代数式表示）；

（2）直线y=kx+b（k＞0）过点B，且与抛物线交于另一点D（点D与点A不重合），交y轴于点C．过点C作CE∥AB交x轴于点E．

（ⅰ） 若∠OBA=90°，2<<3，求k的取值范围；

（ⅱ） 求证：DE∥y轴．

Answer 1

【答案】（1）－；（2）（ⅰ）1＜k＜2；（ⅱ）见解析

【解析】

（1）已知yx2mx，将其化为顶点式，可求得B点坐标，令x2mx＝0可求得OA长，即可用m表示出△OAB的面积．

（2）（ⅰ）如图所示，过点B作BF⊥x轴于点F，可证得△EOC∽△AFB，得出，已知，则，（1）中已得出点B的坐标，且∠OBA90°，得△OAB为等腰直角三角形，列出关于m的方程，求得m值，进而求出BF长，得到OC的取值范围，即为直线ykxb与y轴截距的取值范围，由已知求得的点B坐标，代入直线ykxb，即可得出k的取值范围．

（ⅱ）将用m表示的B点坐标代入直线ykxb中，可将b用m，k表示出来，C点坐标可用m，k表示出来，令抛物线解析式与直线BC解析式相等得到交点D的坐标，再求得AB解析式，根据CE∥AB，即可求得直线CE解析式，得到E点坐标，若点D，E的横坐标相同，即可证得DE∥y轴．

（1）yx2mx＝

∴点B的坐标为B

由x2mx＝0，

得x=0，或x=－m，

∴A(－m,0)

∴OA＝－m

∴S△OAB＝

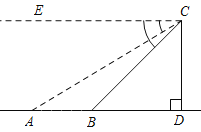
（2）（ⅰ）如图所示，过点B作BF⊥x轴于点F

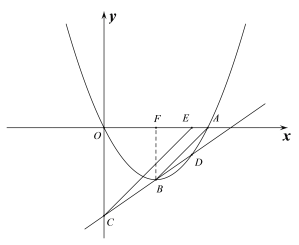
则∠AFB＝∠EOC＝90°

∵CE∥AB

∴∠OEC＝∠FAB

∴△EOC∽△AFB

∴

∵

∴

∵抛物线的顶点坐标为B(,)，∠OBA90°

∴△OAB为等腰直角三角形

∴

∵m≠0

∴m=－2

∴B(1,－1)

∴BF＝1

∴2＜OC＜3

∵点C为直线ykxb与y轴交点

∴2＜－b＜3

∵直线ykxb（k＞0）过点B

∴kb＝－1

∴－b＝k+1

∴2＜k+1＜3

∴1＜k＜2

故答案为：1＜k＜2

（ⅱ）∵直线ykxb（k＞0）过点B(,)

∴

∴

∴ykx

∴C(0,)

由x2mxkx，得

x2(m－k)x－＝0

△＝(m-k)2＋4＝k2

解得x1，x2，

∵点D不与点B重合

∴点D的横坐标为

设直线AB的表达式为y=px+q，则：

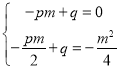
解得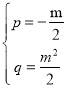

∴直线AB的表达式为y=+

∵直线CE∥AB，且过点C，

∴直线CE的表达式为y=+

当y=0时，x＝

∴E(,0)

∴点D，E的横坐标相同

∴DE∥y轴