题目内容
【题目】在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,且
边上,且![]() 是射线
是射线![]() 上一动点(不与点
上一动点(不与点![]() 重合,且
重合,且![]() ),在射线
),在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
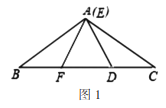
![]() 当点
当点![]() 在线段
在线段![]() 上时,
上时,
①若点![]() 与点
与点![]() 重合时,请说明线段
重合时,请说明线段![]() ;
;
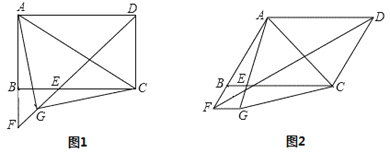
②如图2,若点![]() 不与点
不与点![]() 重合,请说明
重合,请说明![]() ;
;
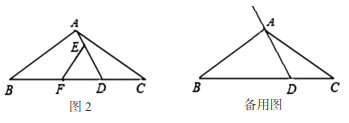
![]() 当点
当点![]() 在线段
在线段![]() 的延长线上
的延长线上![]() 时,用等式表示线段
时,用等式表示线段![]() 之间的数量关系(直接写出结果,不需要证明).
之间的数量关系(直接写出结果,不需要证明).
【答案】(1)①证明见解析;②证明见解析;(2)BF=AE-CD
【解析】
(1)①根据等边对等角,求到![]() ,再由含有60°角的等腰三角形是等边三角形得到
,再由含有60°角的等腰三角形是等边三角形得到![]() 是等边三角形,之后根据等边三角形的性质以及邻补角的性质得到
是等边三角形,之后根据等边三角形的性质以及邻补角的性质得到![]() ,推出
,推出![]() ,根据全等三角形的性质即可得出结论;②过点A做AG∥EF交BC于点G,由△DEF为等边三角形得到DA=DG,再推出AE=GF,根据线段的和差即可整理出结论;
,根据全等三角形的性质即可得出结论;②过点A做AG∥EF交BC于点G,由△DEF为等边三角形得到DA=DG,再推出AE=GF,根据线段的和差即可整理出结论;
(2)根据题意画出图形,作出AG,由(1)可知,AE=GF,DC=BG,再由线段的和差和等量代换即可得到结论.
(1)①证明:![]()
![]()
![]() ,且E与A重合,
,且E与A重合,
![]() 是等边三角形
是等边三角形
![]()
![]()
在![]() 和
和![]() 中
中

![]()
![]()
②如图2,过点A做AG∥EF交BC于点G,

∵∠ADB=60° DE=DF
∴△DEF为等边三角形
∵AG∥EF
∴∠DAG=∠DEF=60°,∠AGD=∠EFD=60°
∴∠DAG=∠AGD
∴DA=DG
∴DA-DE=DG-DF,即AE=GF
由①易证△AGB≌△ADC
∴BG=CD
∴BF=BG+GF=CD+AE
(2)如图3,和(1)中②相同,过点A做AG∥EF交BC于点G,

由(1)可知,AE=GF,DC=BG,
![]()
故![]() .
.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目