题目内容
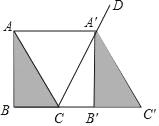
【题目】已知如图,四边形ABCD为平行四边形,AD=a,AC为对角线,BM∥AC,过点D作 DE∥CM,交AC的延长线于F,交BM的延长线于E.
(1)求证:△ADF≌△BCM;
(2)若AC=2CF,∠ADC=60°,AC⊥DC,求四边形ABED的面积(用含a的代数式表示).

【答案】(1)证明见解析.(2)SABED=![]() a2.
a2.
【解析】
(1)由平行线的性质可得∠BMC=∠AFD,∠FAD=∠MBC,进而可得出结论.
(2)可把四边形ABED的面积分解为△ADF的面积与四边形ABEF的面积进行求解.
证明:在平行四边形ABCD中,则AD=BC,AD//BC,
∵AC∥BM,∴∠AFD=∠E,∠DAF=∠ACB,
∵CM∥DE,∴∠BMC=∠E,
∴∠BMC=∠AFD,
∵AC∥BM,
∴∠ACB=∠MBC,
∴∠FAD=∠MBC,
则在△ADF与△BCM中.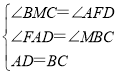 ,
,
∴△ADF≌△BCM(AAS).
(2)解:在△ACD中,
∵AC⊥CD,∠ADC=60°,
∴CD=![]() AD=
AD=![]() a,
a,
则AC=![]() a,
a,
∵AC=2CF,
∴CF=![]() a,
a,
∴AF=![]() =
=![]() =
=![]() a,
a,
又由△ADF≌△BCM,可得BM=![]() a,
a,
又∵DE∥CM,BM∥AC,
∴CFEM为平行四边形,
∴EM=CF=![]() a,
a,
∴BE=BM+EM=![]() a+
a+![]() a=
a=![]() a,
a,
又∵AC⊥DC,
∴DC为△ADF高,
又∵△ADF≌△BCM,
∴△ADF的高的长度等于DC,
SABED=S△ADF+SABEF
=![]() AFCD+
AFCD+![]() (AF+BE)CD
(AF+BE)CD
=![]() ×
×![]() a×
a×![]() a+
a+![]() (
(![]() a+
a+![]() a)×
a)×![]() a
a
=![]() a2.
a2.

练习册系列答案
相关题目