题目内容
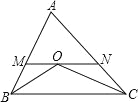
【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.

【答案】0,4,12,16
【解析】
设点E经过t秒时,ΔDEB≌ΔBCA;由斜边ED=CB,分类讨论BE=AC或BE=AB
或AE=0时的情况,求出的值即可.
解:设点E经过t秒时, ΔDEB≌ΔBCA;此时AE=3t
分情况讨论:(1)当点E在点B的左侧时,
BE=24-3t=12,
![]() t=4;
t=4;
(2)当点E在点B的右侧时,
①BE=AC 时,3t=24+12,
![]() t=12;
t=12;
② BE=AB时,
3t=24+24,
![]() t=16.
t=16.
(3)当点E与A重合时,AE=0,t=0;
综上所述,因此, 本题正确答案是:0,4,12,16.

【题目】列方程或方程组解应用题: 在某场CBA比赛中,某位运动员的技术统计如表所示:
技术 | 上场时间(分钟) | 出手投篮(次) | 投中 | 罚球得分(分) | 篮板 | 助攻(次) | 个人总得分(分) |
数据 | 38 | 27 | 11 | 6 | 3 | 4 | 33 |
注:(i)表中出手投篮次数和投中次数均不包括罚球;
(ii)总得分=两分球得分+三分球得分+罚球得分.
根据以上信息,求本场比赛中该运动员投中两分球和三分球各几个.
【题目】某校在学习贯彻十九大精神“我学习,我践行”的活动中,计划组织全校1300名师生到林业部门规划的林区植树,经研究,决定租用当地出租车公司提供的![]() 两种型号的客车共50辆作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量与租车信息:
两种型号的客车共50辆作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量与租车信息:
型号 | 载客量 | 租金单价 |
| 30人/辆 | 300元/辆 |
| 20人/辆 | 240元/辆 |
注:载客量指的是每辆车客车最多可载该校师生的人数
(1)设租用![]() 型号客车
型号客车![]() 辆,租车总费用
辆,租车总费用![]() 元,求
元,求![]() 与
与![]() 的函数解析式,并直接写出
的函数解析式,并直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过13980元,一共有几种租车方案?哪种租车方案最省钱?