题目内容
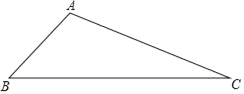
【题目】如图,在四边形ABCD中,∠ABC=90°,DE⊥AC于点E,且AE=CE,DE=5,EB=12. 
(1)求AD的长;
(2)若∠CAB=30°,求四边形ABCD的周长.
【答案】
(1)解:∵∠ABC=90°,AE=CE,EB=12,
∴EB=AE=CE=12.
∵DE⊥AC,DE=5,
∴在Rt△ADE中,
由勾股定理得AD= ![]() =
= ![]() =13
=13
(2)解:∵在Rt△ABC中,∠CAB=30°,AC=AE+CE=24,
∴BC=12,AB=ACcos30°=12 ![]() ,
,
∵DE⊥AC,AE=CE,
∴AD=DC=13,
∴四边形ABCD的周长为AB+BC+CD+AD=38+12 ![]()
【解析】(1)根据等腰三角形的性质和勾股定理即可得到结论;(2)解直角三角形求出各边的长,于是得到结论.
【考点精析】利用勾股定理的概念和解直角三角形对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.