Question

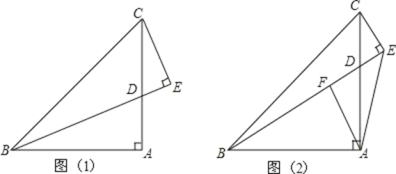
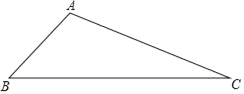
【题目】如图，E 是 BC 的中点，DE 平分∠ADC．

(1)如图 1，若∠B＝∠C＝90°，求证：AE 平分∠DAB；

(2)如图 2，若 DE⊥AE，求证：AD＝AB+CD．

Answer 1

【答案】(1)见解析;(2)见解析.

【解析】

（1）延长 DE 交 AB 的延长线于 F，易得AB∥CD，∠CDE＝∠F，又E 是 BC 的中点，可得E 是 BC 的中点，△CDE≌△BFE，可得DE＝FE，由已知DE 平分∠ADC，可得∠CDE＝∠ADE，∠ADE＝∠F，AD＝AF，可得结论.

（2）在 DA 上截取 DF＝DC，连接 EF, 同理可得△CDE≌△FDE，可得CE＝FE，∠CED＝∠FED，又E 是 BC 的中点，可得FE＝BE，可证得∠AEF＝∠AEB，可得

△AEF≌△AEB 可得AF＝AB，AD＝AF+DF＝AB+CD．

解：（1）如图 1，延长 DE 交 AB 的延长线于 F，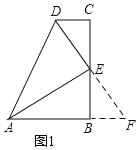

∵∠ABC＝∠C＝90°，

∴AB∥CD，

∴∠CDE＝∠F，

又∵E 是 BC 的中点，

∴E 是 BC 的中点，

∴△CDE≌△BFE（AAS），

∴DE＝FE，即 E 为 DF 的中点，

∵DE 平分∠ADC，

∴∠CDE＝∠ADE，

∴∠ADE＝∠F，

∴AD＝AF，

∴AE 平分∠DAB；

（2）如图 2，在 DA 上截取 DF＝DC，连接 EF，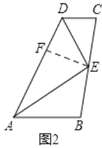

∵DE 平分∠ADC，

∴∠CDE＝∠FDE， 又∵DE＝DE，

∴△CDE≌△FDE（SAS），

∴CE＝FE，∠CED＝∠FED， 又∵E 是 BC 的中点，

∴CE＝BE，

∴FE＝BE，

∵∠AED＝90°，

∴∠AEF+∠DEF＝90°，∠AEB+∠DEC＝90°，

∴∠AEF＝∠AEB， 又∵AE＝AE，

∴△AEF≌△AEB（SAS），

∴AF＝AB，

∴AD＝AF+DF＝AB+CD．