题目内容
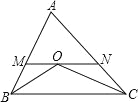
【题目】如图,△ABC 中,BO 平分∠ABC,CO 平分∠ACB,MN 经过点 O,与 AB、AC 相交于点 M、N,且 MN∥BC,那么下列说法中:①∠MOB=∠MBO②△AMN 的周长等于 AB+AC;③∠A=2∠BOC﹣180°;④连接 AO,则![]() :
:![]() :
:![]() =AB:AC:BC;正确的有( )
=AB:AC:BC;正确的有( )
A. ①②④ B. ①②③ C. ①③④ D. ①②③④
【答案】D
【解析】
根据角平分线的定义可得∠ABO=∠CBO,根据两直线平行,内错角相等可得∠CBO=∠BOM,从而得到∠ABO=∠BOM,再根据等角对等边可得BM=OM,同理可得CN=ON,然后即可求出ΔAMN的周长=AB+AC,由ΔABC、ΔBOC内角和为180![]() ,及BO 平分∠ABC,CO 平分∠ACB可得∠A=2∠BOC﹣180
,及BO 平分∠ABC,CO 平分∠ACB可得∠A=2∠BOC﹣180![]() ,可得点O为ΔABC的内心,可得
,可得点O为ΔABC的内心,可得![]() :
:![]() :
:![]() =AB:AC:BC,可得答案.
=AB:AC:BC,可得答案.
解:![]() BO 平分∠ABC,CO 平分∠ACB,
BO 平分∠ABC,CO 平分∠ACB,![]() ∠ABO=∠CBO
∠ABO=∠CBO
![]() MN∥BC,
MN∥BC,![]() ∠CBO=∠BOM,
∠CBO=∠BOM,![]() ∠MOB=∠MBO,故①正确;
∠MOB=∠MBO,故①正确;
![]() BM=OM,同理CN=ON,
BM=OM,同理CN=ON,![]() △AMN 的周长等于 AB+AC,故②正确;
△AMN 的周长等于 AB+AC,故②正确;
![]() 由ΔABC、ΔBOC内角和为180
由ΔABC、ΔBOC内角和为180![]()
![]() ∠A+∠ABC+∠ACB=180
∠A+∠ABC+∠ACB=180![]() ,即:∠A+2(∠OBC+∠OCB)=180
,即:∠A+2(∠OBC+∠OCB)=180![]() ,
,
![]() ∠OBC+∠OCB+∠BOC=180
∠OBC+∠OCB+∠BOC=180![]() ,即∠OBC+∠OCB=180
,即∠OBC+∠OCB=180![]() -∠BOC,
-∠BOC,
可得:∠A=2∠BOC﹣180°,故③正确;
由题意得:点O为ΔABC的内心,设内切圆半径为r,可得![]() :
:![]() :
:![]() =
=![]() AB:
AB:![]() AC:
AC:![]() BC= AB:AC:BC,故④正确
BC= AB:AC:BC,故④正确
故选D.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.