题目内容
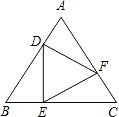
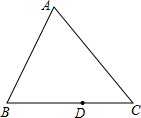
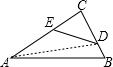
设△ABC的面积是1,D是BC边的三等分点,若在边AC上取一点E,使四边形ABDE的面积为
,则
的值为______.
| 4 |
| 5 |
| AE |
| EC |
连接AD,设△ABD、△ACD、△ADE、△CDE的面积分别为s1、s2、s3、s4,
∵△ABD的边BD上和△ACD的边CD上的高相同,D是BC边的三等分点,由面积公式得:
=
=
,
∵△ABC的面积是1,
∴s1=
,s2=
,
∵四边形ABDE的面积为
,
即s3+s1=
,
∴s3=
,
∴s4=s2-s3=
,
∵△AED的边AE上和△ECD的边CE上的高相同,由面积公式得:
=
=
=
.
设△ABC的BC边上的高为h,BC=a;△CDE的DC边上的高为x,
△CDE面积=
;解得:x=
,
=
,
=
,
故答案为:
,
.
∵△ABD的边BD上和△ACD的边CD上的高相同,D是BC边的三等分点,由面积公式得:
| s1 |
| s2 |
| BD |
| CD |
| 1 |
| 2 |
∵△ABC的面积是1,
∴s1=
| 1 |
| 3 |
| 2 |
| 3 |
∵四边形ABDE的面积为
| 4 |
| 5 |
即s3+s1=
| 4 |
| 5 |
∴s3=
| 7 |
| 15 |
∴s4=s2-s3=
| 3 |
| 15 |
∵△AED的边AE上和△ECD的边CE上的高相同,由面积公式得:
| s3 |
| s4 |
| AE |
| CE |
| ||
|
| 7 |
| 3 |
设△ABC的BC边上的高为h,BC=a;△CDE的DC边上的高为x,
△CDE面积=
| 1 |
| 5 |
| 3h |
| 5 |
| h |
| x |
| AE+EC |
| EC |
| AE |
| EC |
| 2 |
| 3 |
故答案为:
| 7 |
| 3 |
| 2 |
| 3 |


练习册系列答案
相关题目