题目内容
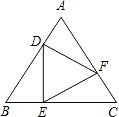
如图，等边△DEF的顶点分别在等边△ABC各边上，且DE⊥BC于E，若AB=1，则DB=______．
∵∠DEB=90°
∴∠BDE=90°-60°=30°
∴∠ADF=180-30°-60°=90°
同理∠EFC=90°
又∵∠A=∠B=∠C，DE=DF=EF
∴△BED≌△ADF≌△CFE
∴AD=BE，
由勾股定理得：
∵BE=
∵AB=BD+AD=BD+BE=BD+
=1
∴BD=
．
∴∠BDE=90°-60°=30°
∴∠ADF=180-30°-60°=90°
同理∠EFC=90°
又∵∠A=∠B=∠C，DE=DF=EF
∴△BED≌△ADF≌△CFE
∴AD=BE，
由勾股定理得：
∵BE=
| BD |
| 2 |
∵AB=BD+AD=BD+BE=BD+
| BD |
| 2 |
∴BD=
| 2 |
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
