题目内容
【题目】如图,在平面直角坐标系x O y中,△ABC 三个顶点坐标分别为A (1, 2),B(7,2),C(5,6).
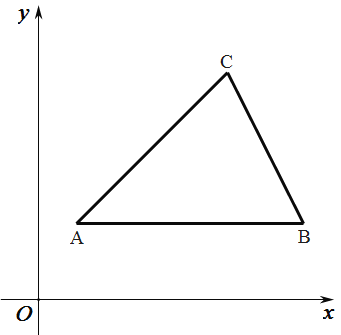
(1)在图中画出△ABC外接圆的圆心P;
(2)圆心P的坐标是______;
(3) tan∠ACB=________.
【答案】(1)详见解析;(2)(4,3);(3)3
【解析】
(1)作AB,AC的中垂线,交于点P,即为所求点;
(2)由A (1, 2),B(7,2),可求出点P的横坐标,设点P的纵坐标为y,连接PA,PC,
由PA=PC,列出关于y的方程,即可求解;
(3)连接AP,BP,作△ABC外接圆,可得:∠ACB=∠APF,进而求出tan∠ACB的值.
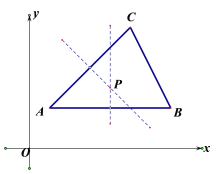
(1)作AB,AC的中垂线,交于点P,即为所求点,如图所示:
(2)∵A (1, 2),B(7,2),C(5,6),
∴点P的横坐标为(1+7)÷2=4,
设点P的纵坐标为y,连接PA,PC,如图1,
∵点P是△ABC外接圆的圆心,
∴PA=PC,
∴![]() ,解得:y=3,
,解得:y=3,
∴点P的坐标是:(4,3),
故答案是:(4,3).
(3)连接AP,BP,作△ABC外接圆,如图2,
∵∠ACB=![]() ∠APB,∠APF=
∠APB,∠APF=![]() ∠APB,
∠APB,
∴∠ACB=∠APF,
∴tan∠ACB= tan∠APF =![]() =
=![]() =3,
=3,
故答案是:3.

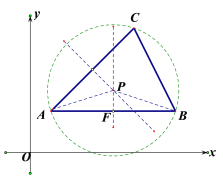
图1 图2

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目