Question

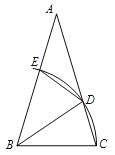
【题目】如图，直线AB经过⊙O上的点C，并且OA＝OB，CA＝CB，⊙O交直线OB于E，D，连接EC，CD．

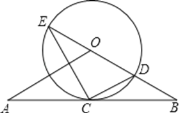
（1）求证：直线AB是⊙O的切线；

（2）试猜想BC，BD，BE三者之间的等量关系，并加以证明；

（3）若tan∠CED＝，⊙O的半径为3，求OA的长．

Answer 1

【答案】（1）见解析；（2）BC2＝BDBE，证明见解析；（3）5

【解析】

（1）连接OC，根据等腰三角形的性质易得OC⊥AB；即可得到证明；

（2）易得∠BCD＝∠E，又有∠CBD＝∠EBC，可得△BCD∽△BEC；故可得BC2＝BDBE；

（3）易得△BCD∽△BEC，BD＝x，由三角形的性质，易得BC2＝BDBE，代入数据即可求出答案．

（1）证明：如图，连接OC，

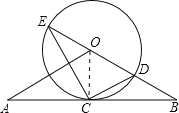
∵OA＝OB，CA＝CB，

∴OC⊥AB，

∴AB是⊙O的切线．

（2）解：BC2＝BDBE．

证明：∵ED是直径，

∴∠ECD＝90°，

∴∠E+∠EDC＝90°．

又∵∠BCD+∠OCD＝90°，∠OCD＝∠ODC（OC＝OD），

∴∠BCD＝∠E．

又∵∠CBD＝∠EBC，

∴△BCD∽△BEC．

∴．

∴BC2＝BDBE．

（3）解：∵tan∠CED＝，

∴．

∵△BCD∽△BEC，

∴．

设BD＝x，则BC＝2x，

∵BC2＝BDBE，

∴（2x）2＝x（x+6）．

∴x1＝0，x2＝2．

∵BD＝x＞0，

∴BD＝2．

∴OA＝OB＝BD+OD＝3+2＝5．