Question

【题目】如图，已知矩形ABCD中，AB=8，AD=6， 点E是边CD上一个动点，连接AE，将△AED沿直线AE翻折得△AEF.

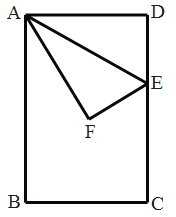
(1) 当点C落在射线AF上时，求DE的长;

(2)以F为圆心，FB长为半径作圆F，当AD与圆F相切时，求cos∠FAB的值;

(3)若P为AB边上一点，当边CD上有且仅有一点Q满∠BQP=45°，直接写出线段BP长的取值范围.

Answer 1

【答案】（1）DE=3；（2） ；（3）BP=12-12或6＜BP≤

【解析】

(1)当点C落在射线AF上时，设DE=x，则EF=DE=x，CE=8-x，根据勾股定理，列出方程，即可求解；

(2)以F为圆心，FB长为半径作圆F，当AD与圆F相切时，设切点为M，连接FM，则FM⊥AD，过点F作FN⊥AB，设FM=x，则AN=FM=x，BF=FM=x，BN=8-x，根据勾股定理，列出方程，即可求解；

(3)以PB为底边作等腰直角三角形PMB，以点M为圆心，MP为半径作圆M，分三类：①当圆M与CD相切时，求出BP的值；②当圆M过点C时，求出BP的值；③当圆M过点D时，求出BP的值，进而，可求出BP的范围.

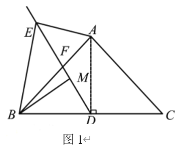
（1）当点C落在射线AF上时，如图1，

∵在矩形ABCD中，AB=8，AD=6，△AED沿直线AE翻折得△AEF，

∴AF=AD=6，AC=，

∴CF=AC-AF=10-6=4，

设DE=x，则EF=DE=x，CE=8-x，

∵在RtCFE中，，

∴，解得：x=3，

∴DE=3；

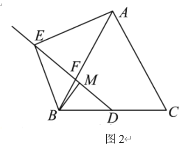
（2）以F为圆心，FB长为半径作圆F，当AD与圆F相切时，如图2，

设切点为M，连接FM，则FM⊥AD，过点F作FN⊥AB，

设FM=x，则AN=FM=x，BF=FM=x，BN=8-x，

∵，

∴，解得：x=，

∴cos∠FAB==；

（3）以PB为底边作等腰直角三角形PMB，以点M为圆心，MP为半径作圆M，

①当圆M与CD相切时，如图3，切点为Q，此时，边CD上有且仅有一点Q满足∠BQP=45°，

连接QM，延长QM交PB于点H，则HQ⊥CD，HQ⊥PB，

∵PMB是等腰直角三角形，

∴设PH=BH=MH=x，则PM=QM=,

∵HQ=AD=6，

∴x+=6，解得：x=，

∴BP=2x=

②当圆M过点C时，如图4，此时，边CD上有两个点Q满足∠BQP=45°，

∵∠MPB=45°，∠PBC=90°，

∴BP=BC=6，

③当圆M过点D时，如图5，此时，边CD上有且仅有一点Q满足∠BQP=45°，

连接MD，过点M作MN⊥AD，MH⊥BP，

设PH=HM=HB=x，则MP=MD=，MN=AH=8-x，ND=6-x，

∵在RtMND中，，

∴，解得：x=，

∴BP=2×=，

综上所述：线段BP长的取值范围是：BP=12-12或6＜BP≤.

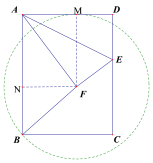
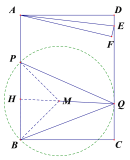
图1 图2 图3

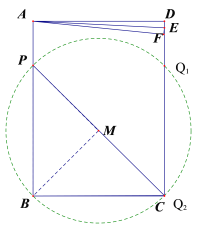
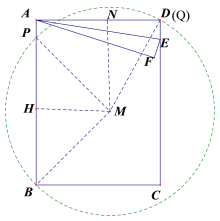
图4 图5