��Ŀ����
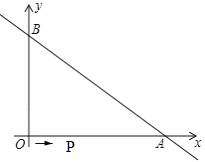
����Ŀ����ͼ��ֱ��![]() ��������ֱ���A��B���㣬OA=8��OB=6������P��O���������·��O��A��B��ÿ��2����λ���ȵ��ٶ��˶�������B��ʱ�˶�ֹͣ��
��������ֱ���A��B���㣬OA=8��OB=6������P��O���������·��O��A��B��ÿ��2����λ���ȵ��ٶ��˶�������B��ʱ�˶�ֹͣ��
(1)��A�������Ϊ_____��B���������Ϊ______��
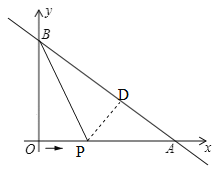
(2)����P��OA�ϣ���BPƽ�֡�OBAʱ�����ʱ��P������Ϊ______��
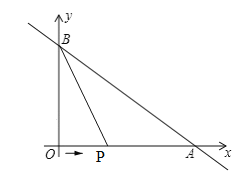
(3)���P���˶�ʱ��Ϊt��(0��t��4)����BPA�����ΪS����S��t֮��ĺ�����ϵʽ����ֱ��д����S=8ʱ��P�����꣮
���𰸡���1����8��0������0��6������2����3��0������3��S=24-6t��0��t��4����P��![]() ��0����
��0����
��������
��1������OA��OB�ij��ȿ����A��B�����������
��2����P��PD��BA��D���ɽ�ƽ���ߵ����ʵõ�PD=OP��ͨ��֤��Rt��BDP��Rt��BOP���õ�BD=OB=6��DA= 4����Rt��PDA�����ɹ��ɶ���������ý�����
��3����0��t��4ʱ��P���߶�OA���˶�����OP=2t��PA=8��2t�����������������ʽ���ɵó���������S=8ʱ���������ʽ�������t��ֵ�������ó�������
��1����OA=8��OB=6����A��8��0����B��0��6����
��2����P��PD��BA��D��
��BPƽ�֡�OBA����PD=OP��
��BP=BP����Rt��BDP��Rt��BOP����BD=OB=6��
��OA=8��OB=6����BA=10����DA=AB��BD=10��6=4��
��Rt��PDA����![]() ����
����![]() �������OP=3����P��3��0����
�������OP=3����P��3��0����
��3����OA=8��v=2����t=8��2=4����P��O�˶���A��ʱ��Ϊ4�����൱0��t��4ʱ��P���߶�OA���˶���
OP=2t��PA=8��OP=8��2t��S=S��BAP=![]() PAOB=
PAOB=![]() ��8-2t��6=24��6t��
��8-2t��6=24��6t��
��S=8ʱ��8=24��6t�������t=![]() ����OP=2t =2��
����OP=2t =2��![]() =
=![]() ����P��
����P��![]() ��0����
��0����
����S= 24��6t��0��t��4������S=8ʱ��P��![]() ��0����
��0����