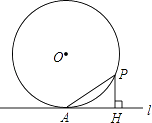题目内容
【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.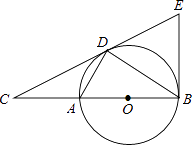
(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求∠BEC的正切值.
【答案】
(1)解:直线CD与⊙O的位置关系是相切.
理由:
连接OD,如图所示:
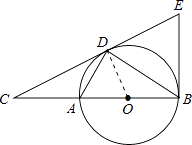
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵∠CDA=∠CBD,
∴∠DAB+∠CDA=90°,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CDA+∠ADO=90°,
即:OD⊥CE,
∴直线CD 是⊙O的切线.
即:直线CD 与⊙O的位置关系是相切.
(2)解:∵AC=2,⊙O的半径是3,
∴OC=2=3=5,OD=3,
在Rt△CDO中,由勾股定理得:CD=4.
∵CE切⊙O于D,EB切⊙O于B,
∴DE=EB,∠CBE=90°,
设DE=EB=x,
在Rt△CBE中,有勾股定理得:CE2=BE2+BC2,
则 (4+x)2=x2+(5+3)2,
解得:x=6,
即 BE=6,
∴tan∠BEC= ![]() ,
,
即:tan∠BEC= ![]() .
.
【解析】(1)连接OD,由直径所对的圆周角为直角得到∠ADB=90°,然后可得到∠CDA+∠ODA=90°,故此可得到直线和圆的位置关系;
(2)首先在Rt△CDO中依据勾股定理求得:CD的长,然后依据切线长定理得DE=EB,设DE=EB=x,在Rt△CBE中,由勾股定理得:CE2=BE2+BC2,可得到关于x的方程,从而可求得x的值,最后由正切函数的定义解得∠BEC的正切值即可.
【考点精析】本题主要考查了直线与圆的三种位置关系和切线的性质定理的相关知识点,需要掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.