题目内容
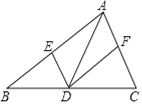
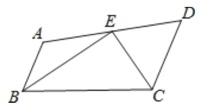
【题目】如图,![]() ,点
,点![]() 是边
是边![]() 上的点,
上的点,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,有下列结论:①
,有下列结论:①![]() ,②
,②![]() 为
为![]() 的中点,③
的中点,③![]() ,④
,④![]() ,其中正确的有______.(填序号)
,其中正确的有______.(填序号)
【答案】②③④
【解析】
根据两直线平行,同旁内角互补可得∠ABC+∠DCB=180°,又BE、CE都是角平分线,可以推出∠EBC+∠ECB=90°,从而得到∠BEC=90°,然后延长BE交CD的延长线于点F,先证明△BCE≌△FFE(ASA),得到BC=FC,BE=FE,然后证明△ABE≌△FDE(ASA),从而可以证明②③正确,AD与BC不一定相等,所以①不正确.
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∵BE平分∠ABC,CE平分∠BCD,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠BCD,
∠BCD,
∴∠EBC+∠ECB=![]() (∠ABC+∠BCD)=90°,
(∠ABC+∠BCD)=90°,
∴∠BEC=180°(∠EBC+∠ECB)=180°90°=90°,
∴BE⊥CE
故④正确;
如图,延长BE交CD延长线于F,
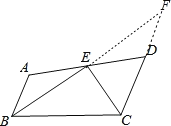
∵∠BEC=90°,
∴CE⊥BF,
∵CE平分∠BCD,
∴∠BCE=∠FCE,
在△BCE与△FCE中,
∠BCE=∠FCE,EC=EC,∠BEC=∠FEC=90°,
∴△BCE≌△FFE(ASA),
∴BC=FC,BE=FE,
∵AB∥CD,
∴∠ABE=∠F,
在△ABE与△FDE中,
∠ABE=∠F,BE=FE,∠AEB=∠FED,
∴△ABE≌△FDE(ASA),
∴AB=DF,
∴BC=CF=CD+DF=CD+AB,故③正确;
∵△ABE≌△FDE,
∴AE=DE,即点E为AD的中点,故②正确;
∵AD≠BC,
∴AD≠CD+AB,故①错误;
故答案为:②③④.

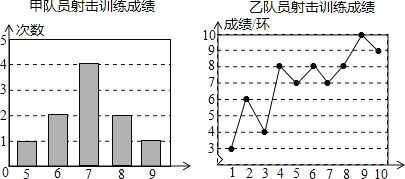
【题目】为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩记录如表:
射击次序(次) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩(环) | 8 | 9 | 7 | 9 | 8 | 6 | 7 | a | 10 | 8 |
乙的成绩(环) | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
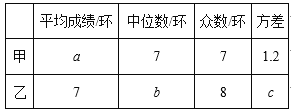
(1)经计算甲和乙的平均成绩是8(环),请求出表中的a= ;
(2)甲成绩的中位数是 环,乙成绩的众数是 环;
(3)若甲成绩的方差是1.2,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?