题目内容
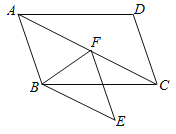
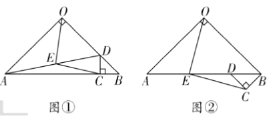
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
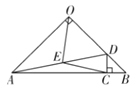
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
【答案】(1)①![]() ;②
;②![]() ;(2)成立,证明见解析;(3)
;(2)成立,证明见解析;(3)![]() 的长为
的长为![]() 或
或![]()
【解析】
(1)①根据直角三角形斜边上的中线等于斜边的一半,即可得到答案;
②由①知![]() ,利用等边对等角和三角形的外角性质,得到
,利用等边对等角和三角形的外角性质,得到![]() ,
,![]() ,然后即可得到答案;
,然后即可得到答案;
(2)①过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,EF与
,EF与![]() 交于点
交于点![]() ,利用等腰直角三角形的性质,证明
,利用等腰直角三角形的性质,证明![]() ,即可得到结论成立;
,即可得到结论成立;
②由全等三角形的性质,求出∠OEC=90°,即可得到结论成立;
(3)根据旋转的性质,点![]() 在同一直线上可分为两种情况:①点C在线段OB上;②点C在OB的延长线上;利用等腰直角三角形的性质,分别求出OE的长度,即可得到答案.
在同一直线上可分为两种情况:①点C在线段OB上;②点C在OB的延长线上;利用等腰直角三角形的性质,分别求出OE的长度,即可得到答案.
解:(1)如图,在△AOD和△ACD中,
∵![]() ,
,![]() 为AD中点,
为AD中点,
![]() ,
,
![]() ,E为AD中点,
,E为AD中点,
![]() ,
,
![]() ;
;
②![]() ,
,![]() 为AD中点,
为AD中点,
![]()
![]() ,
,
∴![]() ;
;
同理可得:![]() ,
,
![]() ,
,
![]() .
.
(2)成立.
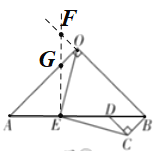
证明:①如图,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 与
与![]() 交于点
交于点![]() ,
,
∵![]() 是等腰三角形,
是等腰三角形,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 均为等腰直角三角形,
均为等腰直角三角形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
②![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)![]() 的长为
的长为![]() 或
或![]() ;
;
∵在等腰直角![]() 中,
中,![]() ,
,
![]() ,
,
由(2)可知,![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ;
;
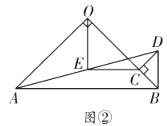
当点![]() 在同一直线上时,有
在同一直线上时,有
①点C在线段OB上;如图:
∴![]() ,
,
∴![]() ;
;
②点C在OB的延长线上;如图:

∴![]() ,
,
∴![]() ;
;
综上所述,![]() 的长为
的长为![]() 或
或![]() ;
;

 名校课堂系列答案
名校课堂系列答案【题目】某商场的运动服装专柜,对![]() 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累计采购款/元 | 10200 | 14400 |
(1)问![]() 两种品牌运动服的进货单价各是多少元?
两种品牌运动服的进货单价各是多少元?
(2)由于![]() 品牌运动服的销量明显好于
品牌运动服的销量明显好于![]() 品牌,商家决定采购
品牌,商家决定采购![]() 品牌的件数比
品牌的件数比![]() 品牌件数的
品牌件数的![]() 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件
倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件![]() 品牌运动服?
品牌运动服?