题目内容
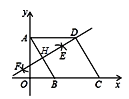
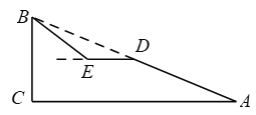
【题目】如图,斜坡AB的长为65米,坡度i=1∶2.4,BC⊥AC.
(参考三角函数:sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() )
)
(1)求斜坡的高度BC.
(2)现计划在斜坡AB的中点D处挖去部分坡体,修建一个平行于水平线CA的平台DE和一条新的斜坡BE,若斜坡BE的坡角为37°,求平台DE的长.
【答案】(1)25;(2)![]() 米
米
【解析】
(1)设BC=x,则AC=2.4x,在Rt△ABC中,利用勾股定理可求得x的值;
(2)如下图,延长DE交BC于F,根据点D是AB的中点,可推导得出点F是BC的中点,从而得出DF,BF的长,然后在Rt△BEF中,求得EF的长,最后得出DE的长.
(1)解:∵斜坡AB的长为65米,坡度i=1∶2.4,
∴可设BC=x,AC=2.4x,
在Rt△ABC中,BC2+AC2=AB2,即得x2+(2.4x)2=652,
解得x=25,
∴BC=25.
(2)解:延长DE交BC于F,
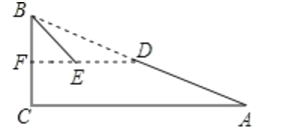
∵D是AB的中点,DE∥AC,∴BF=12.5米,
∴DF=12.5×2.4=30米,
∵tan37°=![]() ,
,
∴EF=![]() 米,
米,
∴DE=DF-EF=![]() 米.
米.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目