题目内容
【题目】已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.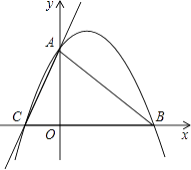
(1)求过A、B、C三点的抛物线的解析式;
(2)若直线CD∥AB交抛物线于D点,求D点的坐标;
(3)若P点是抛物线上的动点,且在第一象限,那么△PAB是否有最大面积?若有,求出此时P点的坐标和△PAB的最大面积;若没有,请说明理由.
【答案】
(1)解:令y=3x+3=0得:x=﹣1,
故点C的坐标为(﹣1,0);
令x=0得:y=3x+3=3×0+3=3
故点A的坐标为(0,3);
∵△OAB是等腰直角三角形.
∴OB=OA=3,
∴点B的坐标为(3,0),
设过A、B、C三点的抛物线的解析式y=ax2+bx+c,
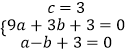
解得: 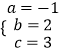
∴解析式为:y=﹣x2+2x+3
(2)解:设直线AB的解析式为y=kx+b,
∴ ![]()
解得: ![]()
∴直线AB的解析式为:y=﹣x+3
∵线CD∥AB
∴设直线CD的解析式为y=﹣x+b
∵经过点C(﹣1,0),
∴﹣(﹣1)+b=0
解得:b=﹣1,
∴直线CD的解析式为:y=﹣x﹣1,
令﹣x﹣1=﹣x2+2x+3,
解得:x=﹣1,或x=4,
将x=4代入y=﹣x2+2x+3=﹣16+2×4+3=﹣5,
∴点D的坐标为:(4,﹣5)
(3)解:存在.如图1所示,设P(x,y)是第一象限的抛物线上一点,
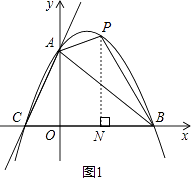
过点P作PN⊥x轴于点N,则ON=x,PN=y,BN=OB﹣ON=3﹣x.
S△ABP=S梯形PNOA+S△PNB﹣S△AOB
= ![]() (OA+PN)ON+
(OA+PN)ON+ ![]() PNBN﹣
PNBN﹣ ![]() OAOB
OAOB
= ![]() (3+y)x+
(3+y)x+ ![]() y(3﹣x)﹣
y(3﹣x)﹣ ![]() ×3×3
×3×3
= ![]() (x+y)﹣
(x+y)﹣ ![]() ,
,
∵P(x,y)在抛物线上,∴y=﹣x2+2x+3,代入上式得:
S△PAB= ![]() (x+y)﹣
(x+y)﹣ ![]() =﹣
=﹣ ![]() (x2﹣3x)=﹣
(x2﹣3x)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时,S△PAB取得最大值.
时,S△PAB取得最大值.
当x= ![]() 时,y=﹣x2+2x+3=
时,y=﹣x2+2x+3= ![]() ,
,
∴P( ![]() ,
, ![]() ).
).
所以,在第一象限的抛物线上,存在一点P,使得△ABP的面积最大;
P点的坐标为( ![]() ,
, ![]() ),最大值为:
),最大值为: ![]()
【解析】(1)先求出直线AC与x轴、y轴的交点的坐标,就可得出点A、C的坐标,再根据△OAB是等腰直角三角形.得出OA=OB,得出点B的坐标,再利用待定系数法就可求出过A、B、C三点的抛物线的解析式。
(2)先利用待定系数法求出直线AB的函数解析式,再根据CD∥AB,可知直线CD的解析式和直线AB的解析式中k值相等,再把点C的坐标代入即可求出直线CD的函数解析式,然后由抛物线的解析式和直线CD的解析式联立方程,解方程就可求出点D的坐标。
(3)抓住已知P点是抛物线上的动点且在第一象限,因此过点P作PN⊥x轴于点N,设P(x,﹣x2+2x+3),用含x的代数式分别表示出ON、PN、BN的长,再根据S△ABP=S梯形PNOA+S△PNB﹣S△AOB建立s与x的函数解析式,求出其顶点坐标,即可得出结果。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a)的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案【题目】下表记录的是今年长江某一周内的水位变化情况,这一周的上周末的水位已达到警戒水位![]() 米(正号表示水位比前一天上升,负号表示水位比前一天下降).
米(正号表示水位比前一天上升,负号表示水位比前一天下降).
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
水位 变化(米) | +0.2 |
| -0.4 |
| +0.3 |
|
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.