Question

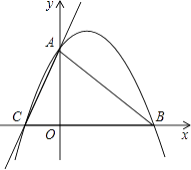
【题目】如图，在平面直角坐标系内，点为坐标原点，点在轴正半轴上，点在轴的负半轴上，点在轴正半轴上，，梯形的面积为，，.

（1）求点，的坐标；

（2）点从点出发以个单位/秒的速度沿向终点运动，同时，点从点出发以个单位秒的速度沿向终点运动，设点的横坐标为，线段的长为，用含的关系式表示，并直接写出相应的范围.

Answer 1

【答案】（1），,（2）当时，；当时，.

【解析】

（1）设AO为x，则BO=AD=x，OC=2x,根据梯形的面积公式列出方程，即可求出x的值，再得出B,C的坐标即可；

（2）根据题意设t秒后P在数轴上表示的数为8-3t,则Q点为-4+t，再根据P、Q相遇前与相遇后分别进行讨论即可.

解：（1）设AO为x，则BO=AD=x，OC=2x,

依题意得

解得x=4，（x=-4舍去）

∴，.

（2）设t秒后P在数轴上表示的数为8-3t,则Q点为-4+t，

①P、Q相遇前：

即时，d=PQ=(8-3t)-( -4+t)=12-4t,

又m=8-3t,

∴；

②P、Q相遇后，即当时，且P,Q分别在B,C处停下，

d=PQ=( -4+t)-(8-3t) =-12+4t,

m=8-3t,

∴.

故当时，；当时，.