题目内容
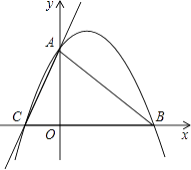
【题目】如图，在平面直角坐标系xOy中，⊙A与y轴相切于点B（0， 
），与x轴相交于M，N两点，如果点M的坐标为（ 
，0），求点N的坐标
【答案】解：连接AB、AM、过A作AC⊥MN于C，设⊙A的半径是R，
∵⊙A与y轴相切于B，
∴AB⊥y轴，
∵点B（0， 
），与x轴相交于M、N两点，点M的坐标为（ 
，0），
∴AB=AM=R，CM=R- ，AC= ，MN=2CM，
由勾股定理得：R2=（R- ）2+（ ）2，
R=2．5，
∴CM=CN=2．5- =2，
∴ON= +2+2=4 ，
即N的坐标是（4 ，0）．
【解析】要求点N的坐标，就需求出MN的长，因此过A作AC⊥MN于C，连接AB、AM、先由点B的坐标，就可求出AC的长，AB=OC=R，由点M的坐标就可求出OM的长，表示出MC的长，根据勾股定理求出R的长，即可求出MN的长，从而得出点N的坐标。
【考点精析】根据题目的已知条件，利用勾股定理的概念和垂径定理的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
阳光课堂课时优化作业系列答案【题目】某商场销售A，B两种品牌的教学设备，这两种教学设备的进价和售价如下表所示：
A | B | |
进价（万元/套） | 1.5 | 1.2 |
售价（万元/套） | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套，共需66万元，全部销售后可获毛利润9万元。
（毛利润=（售价 - 进价）×销售量）
（1）该商场计划购进A，B两种品牌的教学设备各多少套？
（2）通过市场调研，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元，问A种设备购进数量至多减少多少套？
