��Ŀ����
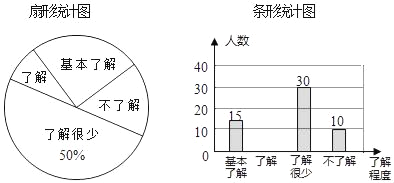
����Ŀ����У��ȫ���ܵ�ȫ���Ĺ㷺��ע������ij��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ���������ͼ�����в�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ����������⣺
��1�������ʾ������ѧ�������� ���ˣ�����ͳ��ͼ�����˽�����������Ӧ���ε�Բ�Ľ�Ϊ�� ���㣻
��2��������ѧ����ѧ��900�ˣ���������������������Ƹ���ѧѧ���ж�У��ȫ֪ʶ�ﵽ���˽������������˽����̶ȵ�������Ϊ�� �ˣ�
��3�����Ӷ�У��ȫ֪ʶ�ﵽ���˽����̶ȵ�3��Ů��A��B��C��2������M��N�зֱ������ȡ1�˲μ�У��ȫ֪ʶ������������״ͼ���б������ǡ�ó鵽Ů��A�ĸ��ʣ�
���𰸡���1��60��30������2��300����3��![]()
��������
��1�����˽���ٵ���30�ˣ�ռ50%������ý����ʾ������ѧ�������̶��������ͳ��ͼ�С��˽⡱��������Ӧ���ε�Բ�Ľǣ�
��2������������������ķ�����������ô𰸣�
��3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����ǡ�ó鵽Ů��A������������ø��ʹ�ʽ��⼴����ô𰸣�
�⣺��1�����˽���ٵ���30�ˣ�ռ50%��
�������ʾ������ѧ�����У�30��50%=60���ˣ���
���˽ⲿ�ֵ�����Ϊ60����15+30+10��=5��
������ͳ��ͼ�����˽�����������Ӧ���ε�Բ�Ľ�Ϊ��![]() ��360��=30�㣻
��360��=30�㣻
�ʴ�Ϊ��60��30��
��2����������ã�900��![]() =300���ˣ���
=300���ˣ���
����Ƹ���ѧѧ���ж�У��ȫ֪ʶ�ﵽ���˽������������˽����̶ȵ�������Ϊ300�ˣ�
�ʴ�Ϊ��300��
��3������״ͼ���£�
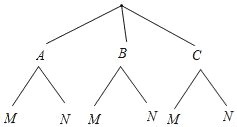
���еȿ��ܵ������6�֣����г鵽Ů��A�������2�֣�
����P���鵽Ů��A��=![]() =
=![]() ��
��