题目内容
【题目】如图,在平行四边形ABCD中,AC,BD相交于点O,AC=6,BD=8,∠AOD=65°,点E在BO上,AF∥CE交BD于点F.
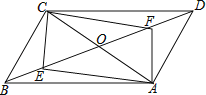
(1)求证:四边形AFCE是平行四边形.
(2)当点E在边BO上移动时,平行四边形AFCE能否为矩形?若能,此时BE的长为多少(直接写出结果)?若不能,请说明理由.
(3)当点E在边BO上移动时,平行四边形AFCE能否为菱形?若能,此时BE的长为多少(直接写出结果)?若不能,请说明理由.
【答案】(1)见解析;(2)平行四边形AFCE能为矩形,此时BE=1;(3)平行四边形AFCE不能为菱形,理由见解析.
【解析】
(1)四边形ABCD为平行四边形,又AF∥CE,易证得△AOF≌△COE,则可得OE=OF,又由OA=OC,即可判定四边形AFCE是平行四边形;
(2)当EF=AC时,平行四边形AFCE为矩形,先得出BE=DF,再由AC=EF=6,BD=8,即可求得此时BE的长;
(3)由∠AOD=65°,可得AC与BD不垂直,即可得平行四边形AFCE不能为菱形.
(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AF∥CE,
∴∠OAF=∠OCE,
在△AOF和△COE中,
 ,
,
∴△AOF≌△COE(ASA),
∴OE=OF,又OA=OC,
∴四边形AFCE是平行四边形;
(2)解:平行四边形AFCE能为矩形.
理由:∵四边形AFCE是平行四边形,
∴当EF=AC=6时,平行四边形AFCE为矩形,
∴OE=OF,又OB=OD,
∴BE=DF,
∴2BE+EF=BD,
即2BE+6=8,
解得:BE=1,
∴当BE=1时,平行四边形AFCE为矩形;
(3)解:平行四边形AFCE不能为菱形.
理由:∵四边形AFCE是平行四边形,且∠AOD=65°,
即AC与BD不垂直,
∴平行四边形AFCE不能为菱形.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案【题目】某天,一蔬菜经营户用 1200 元钱按批发价从蔬菜批发市场买了西红柿和豆角共 400 kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 2.4 | 3.2 |
零售价(单位:元/kg) | 3.8 | 5.2 |
(1)该经营户所批发的西红柿和豆角的质量分别为多少 kg?
(2)如果西红柿和豆角全部以零售价售出,他当天卖出这些西红柿和豆角赚了多少钱?