Question

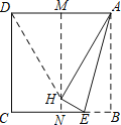
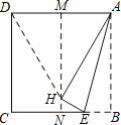
【题目】 如图，先将正方形纸片对折，折痕为MN，再把点B折叠在折痕MN上，折痕为AE，点E在CB上，点B在MN上的对应点为H，连接DH，则下列选项错误的是（　　）

A.△ADH是等边三角形B.NE=BC

C.∠BAE=15°D.∠MAH+∠NEH=90°

Answer 1

【答案】B

【解析】

依据折叠的性质以及正方形的性质，得到△ADH是等边三角形；依据AM=AD=AH，得到∠AHM=30°，进而得出∠BAE=15°；依据∠AHE=∠B=90°，∠AMH=∠ENH=90°，即可得到∠MAH+∠NEH=90°．

由折叠可得，MN垂直平分AD，AB=AH，

∴DH=AH=AB=AD，

∴△ADH是等边三角形，故A选项正确；

∵BE=HE＞NE，

∴BE＞BN，

∴NE=BC不成立，故B选项错误；

由折叠可得，AM=AD=AH，

∴∠AHM=30°，∠HAM=60°，

又∵∠BAD=90°，

∴∠BAH=30°，

由折叠可得，∠BAE=∠BAH=15°，故C选项正确；

由折叠可得，∠AHE=∠B=90°，

又∵∠AMH=90°，

∴∠AHM+∠HAM=90°，∠AHM+∠EHN=90°，

∴∠HAM=∠EHN，

同理可得∠NEH+∠AHM，

∴∠MAH+∠NEH=90°，故D选项正确；

故选：B．