Question

【题目】如图，在中，已知，的垂直平分线交于点，交于点，连接.

（1）若，则的度数是 ；

（2）若，的周长是.

①求的长度；

②若点为直线上一点，请你直接写出周长的最小值.

Answer 1

【答案】（1）；（2）①6；②．

【解析】

（1）根据等腰三角形的性质和线段垂直平分线的性质即可得到结论；
（2）①根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AM=BM，然后求出△MBC的周长=AC+BC，再代入数据进行计算即可得解；
②当点P与M重合时，△PBC周长的值最小，于是得到结论．

解：解：（1）如图，

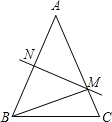
∵AB=AC，
∴∠C=∠ABC=70°，
∴∠A=40°，
∵AB的垂直平分线交AB于点N，
∴∠ANM=90°，
∴∠NMA=50°，
故答案为：50；
（2）①∵MN是AB的垂直平分线，
∴AM=BM，
∴△MBC的周长=BM+CM+BC=AM+CM+BC=AC+BC，
∵AB=8，

∴AC=8，

∵△MBC的周长是14，
∴BC=14-8=6；
②∵PB+PC=PA+PC，PA+PC≥AC，
∴当点P与M重合时，PA+PC=AC，此时PB+PC最小，
∴△PBC周长的最小值=AC+BC=8+6=14．