题目内容
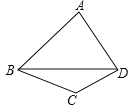
【题目】已知:如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作
为直径作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 和
和![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求线段
,求线段![]() 的长;
的长;
(3)在![]() 的条件下,求
的条件下,求![]() 的面积.
的面积.

【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据圆周角定理可得∠ADB=90°,由等腰三角形三线合一可得∠ABD=∠CBD,又AD、DE是两角对应的弦,所以可证AD=DE;(2)先证△CED∽△CAB,再根据相似三角形的性质和已知边长求得CD;(3)在Rt△ABD中由勾股定理求得BD,根据角相等,可证△BPE∽△BED,利用相似性质求得BP,进一步求得DP,根据等高三角形面积比等于底边的比,可得S△BCD:S△BPE=DP:BP=13:32,,S△BDE:S△BCD=BE:BC=4:5,再根据三角形面积公式即可求解.
(1)证明:∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∵![]() ,
,
∴![]() 是
是![]() 的中点,
的中点,![]() ,
,
∴![]() ;
;
(2)∵四边形![]() 内接于
内接于![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]() ;
;
(3)延长![]() 交
交![]() 于
于![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目