Question

【题目】在中，，，．

如图①，将线段绕点顺时针旋转，所得到与交于点，则的长________；

如图②，点是边上一点且，将线段绕点旋转，得线段，点始终为的中点，则将线段绕点逆时针旋转________度时，线段的长最大，最大值为________．

Answer 1

【答案】6 180

【解析】

（1）根据旋转的性质及等腰三角形、等边三角形的性质求解．
（2）当将线段AD绕点A逆时针旋转180度时，线段CF的长最大，此时所求CF是Rt△BCD′的斜边上的中线，它等于斜边的一半．

(Ⅰ)如下图①所示：

∵将线段CA绕点C顺时针旋转，

∴△AMC为等腰三角形，AM=MC

∵∠BAC=，

∴△MBC为等边三角形，

∴AM=MB=CM

又∵BC=6，

∴AB=2BC=12，

∴CM=6

故答案为：6

(2)∵在RtABC中,∠ACB=,BAC=，BC=6，

∴

当将线段AD绕点A逆时针旋转180度时，线段CF的长最大，如图②所示：

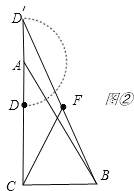
∵AD=AD′，

∴

∵在RtABC中,

∴

∵点F是BD′的中点，

∴

即：当将线段AD绕点A逆时针旋转180度时,线段CF的长最大,最大值为

故答案为：180;.