题目内容
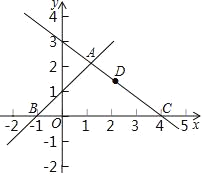
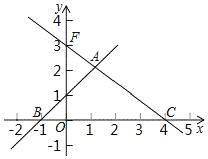
【题目】如图,在平面直角坐标系可中,直线y=x+1与y=﹣![]() x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
(1)求点A,B,C的坐标;
(2)在直线AB上是否存在点E使得四边形EODA为平行四边形?存在的话直接写出![]() 的值,不存在请说明理由;
的值,不存在请说明理由;
(3)当△CBD为等腰三角形时直接写出D坐标.
【答案】(1)A(![]() ,
,![]() ),B(﹣1,0),C(4,0);(2)存在,
),B(﹣1,0),C(4,0);(2)存在,![]() =
=![]() ;(3)点D的坐标为(﹣
;(3)点D的坐标为(﹣![]() ,
,![]() )或(8,﹣3)或(0,3)或(
)或(8,﹣3)或(0,3)或(![]() ,
,![]() ).
).
【解析】
(1)将y=x+1与y=﹣![]() x+3联立求得方程组的解可得到点A的坐标,然后将y=0代入函数解析式求得对应的x的值可得到点B、C的横坐标;
x+3联立求得方程组的解可得到点A的坐标,然后将y=0代入函数解析式求得对应的x的值可得到点B、C的横坐标;
(2)当OE∥AD时,存在四边形EODA为平行四边形,然后依据平行线分线段成比例定理可得到![]() =
=![]() ;
;
(3)当DB=DC时,点D在BC的垂直平分线上可先求得点D的横坐标;即AC与y轴的交点为F,可求得CF=BC=F,当点D与点F重合或点D与点F关于点C对称时,三角形BCD为等腰三角形,当BD=BC时,设点D的坐标为(x,﹣![]() x+3),依据两点间的距离公式可知:(x+1)2+(﹣
x+3),依据两点间的距离公式可知:(x+1)2+(﹣![]() x+3)2=25,从而可求得点D的横坐标.
x+3)2=25,从而可求得点D的横坐标.
(1)将y=x+1与y=﹣![]() x+3联立得:
x+3联立得: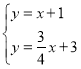 ,
,
解得:x=![]() ,y=
,y=![]() ,
,
∴A(![]() ,
,![]() ).
).
把y=0代入y=x+1得:x+1=0,解得x=﹣1,
∴B(﹣1,0).
把y=0代入y=﹣![]() x+3得:﹣
x+3得:﹣![]() x+3=0,解得:x=4,
x+3=0,解得:x=4,
∴C(4,0).
(2)如图,存在点E使EODA为平行四边形.

∵EO∥AC,
∴![]() =
=![]() =
=![]() .
.
(3)当点BD=DC时,点D在BC的垂直平分线上,则点D的横坐标为![]() ,
,
将x=![]() 代入直线AC的解析式得:y=
代入直线AC的解析式得:y=![]() ,
,
∴此时点D的坐标为(![]() ,
,![]() ).
).
如图所示:
FC=![]() =5,
=5,
∴BC=CF,
∴当点D与点F重合时,△BCD为等腰三角形,
∴此时点D的坐标为(0,3);
当点D与点F关于点C对称时,CD=CB,
∴此时点D的坐标为(8,﹣3),
当BD=DC时,设点D的坐标为(x,﹣![]() x+3),
x+3),
依据两点间的距离公式可知:(x+1)2+(﹣![]() x+3)2=25,
x+3)2=25,
解得x=4(舍去)或x=﹣![]() ,
,
将x=﹣![]() 代入y=﹣
代入y=﹣![]() x+3得y=
x+3得y=![]() ,
,
∴此时点D的坐标为(﹣![]() ,
,![]() ).
).
综上所述点D的坐标为(﹣![]() ,
,![]() )或(8,﹣3)或(0,3)或(
)或(8,﹣3)或(0,3)或(![]() ,
,![]() ).
).

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】某公园的门票价格如下表所示:
购票人数 | 1~50人 | 51~100人 | 100人以上 |
每人门票价 | 20元 | 17元 | 14元 |
某校初一(1)(2)两个班去游览公园,其中(1)班人数较少,不足50人,(2)班人数较多,超过50人,但是不超过100人.如果两个班都以班为单位分别购票,则一共应付1912元;如果两个班联合起来,作为个团体购票,则只需付1456元
(1)列方程或方程组求出两个班各有多少学生?
(2)若(1)班全员参加,(2)班有20人不参加此次活动,请你设计一种最省钱方式来帮他们买票,并说明理由.
(3)你认为是否存在这样的可能:51到100人之间买票的钱数与100人以上买票的钱数相等?如果有,是多少人与多少人买票钱数相等?(直接写结果)
【题目】某校为了调查学生书写规范汉字的能力,从七年级1000名学生中随机抽选了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整)
组别 | 成绩x分 | 频数(人数) |
第1组 | x<60 | 4 |
第2组 | 60≤x<70 | a |
第3组 | 70≤x<80 | 20 |
第4组 | 80≤x<90 | b |
第5组 | 90≤x<100 | 10 |

请结合图表完成下列各题
(1)填空:表中a的值为_______,b的值为_______,扇形统计图中表示第1组所对应的圆心角度数为_______.
(2)若测试成绩不低于80分为优秀,请你估计从该校七年级学生中随机抽查一个学生,他是规范汉字书写优秀的概率是_______;
(3)若测试成绩在60~80分之间(含60分,不含80分)为合格,请你估计则该校七年级学生规范汉字书写不合格的人数.