题目内容
【题目】某公园的门票价格如下表所示:
购票人数 | 1~50人 | 51~100人 | 100人以上 |
每人门票价 | 20元 | 17元 | 14元 |
某校初一(1)(2)两个班去游览公园,其中(1)班人数较少,不足50人,(2)班人数较多,超过50人,但是不超过100人.如果两个班都以班为单位分别购票,则一共应付1912元;如果两个班联合起来,作为个团体购票,则只需付1456元
(1)列方程或方程组求出两个班各有多少学生?
(2)若(1)班全员参加,(2)班有20人不参加此次活动,请你设计一种最省钱方式来帮他们买票,并说明理由.
(3)你认为是否存在这样的可能:51到100人之间买票的钱数与100人以上买票的钱数相等?如果有,是多少人与多少人买票钱数相等?(直接写结果)
【答案】(1)初一(1)班有48人,初一(2)班有56人;(2)两个班联合起来买101张门票最省钱;理由见解析;(3)84人和102人或98人和119人买票钱数相等.
【解析】
(1)由两班人数之和为整数可得出初一(1)(2)两个班的人数之和大于100,设初一(1)班有![]() 人,初一(2)班有y人,根据总价=单价×数量,即可得出二元一次方程组,解之即可;
人,初一(2)班有y人,根据总价=单价×数量,即可得出二元一次方程组,解之即可;
(2)求出参加活动的人数,利用总价=单价×数量,分别求出购买84张门票及101张门票所需钱数,比较后即可得出结论;
(3)设m人与n人买票钱数相等(51≤m≤100,n≥101),根据总价=单价×数量且总价相等,即可得出关于m,n的二元一次方程,结合m,n为正整数及其范围,即可求出m,n的值.
(1)如果初一(1)(2)两个班的人数之和不大于100,
则1456÷17=85(人)![]() (元),不符合题意,
(元),不符合题意,
∴初一(1)(2)两个班的人数之和大于100.
设初一(1)班有x人,初一(2)班有y人,
依题意,得: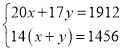 ,
,
解得:![]() ;
;
答:初一(1)班有48人,初一(2)班有56人;
(2)48+(56﹣20)=84(人).
两个班合起来买84张门票所需钱数为:84×17=1428(元),
两个班合起来买101张门票所需钱数为:101×14=1414(元),
∵1414<1428,
∴两个班合起来买101张门票最省钱;
(3)设m人与n人买票钱数相等(51≤m≤100,n≥101),
依题意,得:17m=14n,
∴m为14的整数倍,n为17的整数倍,
∴![]() 或
或![]() .
.
答:84人和102人或98人和119人买票钱数相等.