题目内容
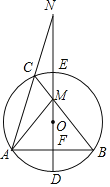
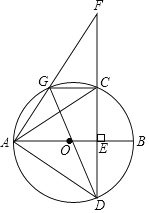
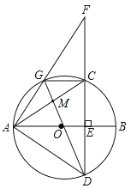
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,G是![]() 上一动点,AG,DC的延长线交于点F,连接AC,AD,GC,GD.
上一动点,AG,DC的延长线交于点F,连接AC,AD,GC,GD.
(1)求证:∠FGC=∠AGD;
(2)若AD=6.
①当AC⊥DG,CG=2时,求sin∠ADG;
②当四边形ADCG面积最大时,求CF的长.
【答案】(1)证明见解析;(2)①sin∠ADG=![]() ;②CF=6.
;②CF=6.
【解析】
(1)由垂径定理可得CE=DE,CD⊥AB,由等腰三角形的性质和圆内接四边形的性质可得∠FGC=∠ADC=∠ACD=∠AGD;
(2)①如图,设AC与GD交于点M,证△GMC∽△AMD,设CM=x,则DM=3x,在Rt△AMD中,通过勾股定理求出x的值,即可求出AM的长,可求出sin∠ADG的值;
②S四边形ADCG=S△ADC+S△ACG,因为点G是![]() 上一动点,所以当点G在
上一动点,所以当点G在![]() 的中点时,△ACG的的底边AC上的高最大,此时△ACG的面积最大,四边形ADCG的面积也最大,分别证∠GAC=∠GCA,∠F=∠GCA,推出∠F=∠GAC,即可得出FC=AC=6.
的中点时,△ACG的的底边AC上的高最大,此时△ACG的面积最大,四边形ADCG的面积也最大,分别证∠GAC=∠GCA,∠F=∠GCA,推出∠F=∠GAC,即可得出FC=AC=6.
证明:(1)∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DE,CD⊥AB,
∴AC=AD,
∴∠ADC=∠ACD,
∵四边形ADCG是圆内接四边形,
∴∠ADC=∠FGC,
∵∠AGD=∠ACD,
∴∠FGC=∠ADC=∠ACD=∠AGD,
∴∠FGC=∠AGD;
(2)①如图,设AC与GD交于点M,
∵![]() ,
,
∴∠GCM=∠ADM,
又∵∠GMC=∠AMD,
∴△GMC∽△AMD,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
设CM=x,则DM=3x,
由(1)知,AC=AD,
∴AC=6,AM=6﹣x,
在Rt△AMD中,
AM2+DM2=AD2,
∴(6﹣x)2+(3x)2=62,
解得,x1=0(舍去),x2=![]() ,
,
∴AM=6﹣![]() =
=![]() ,
,
∴sin∠ADG=![]() =
=![]() =
=![]() ;
;
②S四边形ADCG=S△ADC+S△ACG,
∵点G是![]() 上一动点,
上一动点,
∴当点G在![]() 的中点时,△ACG的底边AC上的高最大,此时△ACG的面积最大,四边形ADCG的面积也最大,∴GA=GC,
的中点时,△ACG的底边AC上的高最大,此时△ACG的面积最大,四边形ADCG的面积也最大,∴GA=GC,
∴∠GAC=∠GCA,
∵∠GCD=∠F+∠FGC,
由(1)知,∠FGC=∠ACD,且∠GCD=∠ACD+∠GCA,
∴∠F=∠GCA,
∴∠F=∠GAC,
∴FC=AC=6.

 名校课堂系列答案
名校课堂系列答案