题目内容
【题目】如图,在平面直角坐标系中,以点M(0, ![]() )为圆心,以
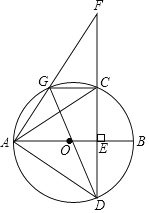
)为圆心,以![]() 长为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
长为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
(1)求出CP所在直线的解析式;
(2)连接AC,请求△ACP的面积.

【答案】(1)直线CP的解析式为y=3x-3;(2)△ACP的面积=12ACPC=12×23×6=63.
【解析】
试题(1)要求CP所在的直线的解析式,就必须知道C,P两点的坐标,有圆心M的坐标,有圆的半径,那么可求出OC的,OM的长,直角三角形AMO中有AM,OM的值,就能求出OA,OB的长,那么P的横坐标就求出来了,连接PB,那么OM是三角形APB的中位线,PB=2OM,已经求出了OM的长,那么PB的长也就求出来了,这样P点的坐标就求出来了,有了C,P的坐标,可根据待定系数法求出CP所在直线的解析式;
(2)求三角形ACP的面积实际上是求直角边AC,PC的长,因为三角形ACP是个直角三角形,有斜边AB的长,只要求出这个三角形中锐角的度数,即可求出直角边的长,在三角形AMO中,我们可求出∠AMO的度数,根据圆周角定理,也就求出了∠P的度数,有了锐角的度数和斜边的长,直角边就能求出来了,面积也就能求出来了.
试题解析: (1)连接PB,
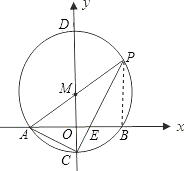
∵PA是⊙M的直径,
∴∠PBA=90°,
∵DC是⊙M的直径,且垂直于弦AB,
∴DC平分弦AB,
在Rt△AMO中AM=2![]() ,OM=
,OM=![]() ,
,
∴AO=OB=3,
又∵MO⊥AB,
∴PB∥MO,
∴PB=2OM=2![]() ,
,
∴P点坐标为(3,2![]() ),
),
∵CM=2![]() ,OM=
,OM=![]() ,
,
∴OC=CMOM=![]() ,
,
∴C(0,![]() ),直线CP过C,P两点,
),直线CP过C,P两点,
设直线CP的解析式为y=kx+b(k≠0),
得到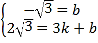 ,
,
解得: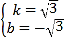 ,
,
∴直线CP的解析式为y=![]() x
x![]() ;
;
(2)在Rt△AMO中,∠AMO=60°,
又∵AM=CM,
∴△AMC为等边三角形,
∴AC=AM=2![]() ,∠MAC=60°
,∠MAC=60°
又∵AP为⊙M的直径,
∴∠ACP=90°,∠APC=30°,
PC=![]() AC=
AC=![]() ×2
×2![]() =6,
=6,
∴△ACP的面积=![]() ACPC=
ACPC=![]() ×2
×2![]() ×6=6
×6=6![]() .
.

 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案