ЬтФПФкШн
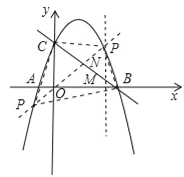
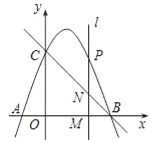
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпy=Љx+3гыxжсЁЂyжсЗжБ№НЛгкЕуBЁЂCЃЛХзЮяЯпy=Љx2+bx+cОЙ§BЁЂCСНЕуЃЌВЂгыxжсНЛгкСэвЛЕуAЃЎ
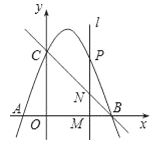
ЃЈ1ЃЉЧѓИУХзЮяЯпЫљЖдгІЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЩшPЃЈxЃЌyЃЉЪЧЃЈ1ЃЉЫљЕУХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїжБЯпlЁЭxжсгкЕуMЃЌНЛжБЯпBCгкЕуNЃЎ
ЂйШєЕуPдкЕквЛЯѓЯоФкЃЎЪдЮЪЃКЯпЖЮPNЕФГЄЖШЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧѓГіЫќЕФзюДѓжЕМАДЫЪБxЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЂкЧѓвдBCЮЊЕзБпЕФЕШбќЁїBPCЕФУцЛ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЫљЧѓКЏЪ§ЙиЯЕЪНЮЊy=Љx2+2x+3ЃЛ
ЃЈ2ЃЉЂйЯпЖЮPNЕФГЄЖШЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
Ђк![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉРћгУвЛДЮКЏЪ§гызјБъжсзјБъЧѓЗЈЃЌЕУГіBЁЂCСНЕуЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіЖўДЮКЏЪ§НтЮіЪНЃЎ
ЃЈ2ЃЉРћгУЖўДЮКЏЪ§зюжЕЧѓЗЈВЛФбЧѓГіЃЌдйРћгУШ§НЧаЮУцЛ§жЎМфЕФЙиЯЕЃЌПЩЧѓГіЕШбќЁїBPCЕФУцЛ§
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩгкжБЯпy=Љx+3ОЙ§BЁЂCСНЕуЃЌ
Сюy=0ЕУx=3ЃЛСюx=0ЃЌЕУy=3ЃЌ
ЁрBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉЃЌ
ЁпЕуBЁЂCдкХзЮяЯпy=Љx2+bx+cЩЯЃЌгкЪЧЕУ![]() ЃЌ
ЃЌ
НтЕУb=2ЃЌc=3ЃЌ
ЁрЫљЧѓКЏЪ§ЙиЯЕЪНЮЊy=Љx2+2x+3ЃЛ
ЃЈ2ЃЉЂйЁпЕуPЃЈxЃЌyЃЉдкХзЮяЯпy=Љx2+2x+3ЩЯЃЌ
ЧвPNЁЭxжсЃЌ
ЁрЩшЕуPЕФзјБъЮЊЃЈxЃЌЉx2+2x+3ЃЉЃЌ
ЭЌРэПЩЩшЕуNЕФзјБъЮЊЃЈxЃЌЉx+3ЃЉЃЌ
гжЕуPдкЕквЛЯѓЯоЃЌ
ЁрPN=PMЉNMЃЌ
=ЃЈЉx2+2x+3ЃЉЉЃЈЉx+3ЃЉЃЌ
=Љx2+3xЃЌ
=ЁЊ![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ
ЯпЖЮPNЕФГЄЖШЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЂкНтЃК
гЩЬтвтжЊЃЌЕуPдкЯпЖЮBCЕФДЙжБЦНЗжЯпЩЯЃЌ
гжгЩЂйжЊЃЌOB=OCЃЌ
ЁрBCЕФжаДЙЯпЭЌЪБвВЪЧЁЯBOCЕФЦНЗжЯпЃЌ
ЁрЩшЕуPЕФзјБъЮЊЃЈaЃЌaЃЉЃЌ
гжЕуPдкХзЮяЯпy=Љx2+2x+3ЩЯЃЌгкЪЧгаa=Љa2+2a+3ЃЌ
Ёрa2ЉaЉ3=0ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊЃК![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ШєЕуPЕФзјБъЮЊ![]() ЃЌДЫЪБЕуPдкЕквЛЯѓЯоЃЌ
ЃЌДЫЪБЕуPдкЕквЛЯѓЯоЃЌ
дкRtЁїOMPКЭRtЁїBOCжаЃЌMP=OM=![]() ЃЌ
ЃЌ
OB=OC=3ЃЌ
SЁїBPC=SЫФБпаЮBOCPЉSЁїBOC=2SЁїBOPЉSЁїBOCЃЌ
=![]() ЃЌ
ЃЌ
ШєЕуPЕФзјБъЮЊ![]() ЃЌДЫЪБЕуPдкЕкШ§ЯѓЯоЃЌ
ЃЌДЫЪБЕуPдкЕкШ§ЯѓЯоЃЌ
дђSЁїBPC=SЁїBOP+SЁїCOP+SЁїBOC=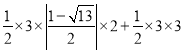 ЃЌ
ЃЌ
=![]() ЃЌ
ЃЌ