Question

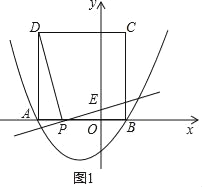
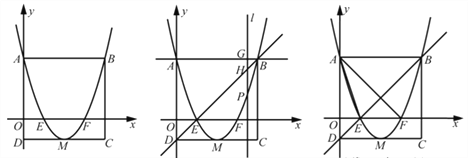
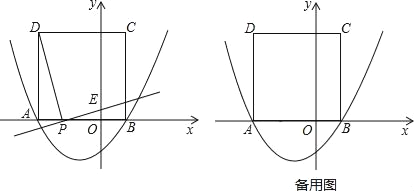
【题目】如图，已知二次函数y=x2+bx﹣与x轴交于点A（﹣3，0）和点B，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接DP，过点P作DP的垂线与y轴交于点E．

（1）试求出二次函数的表达式和点B的坐标；

（2）当点P在线段AO（点P不与A、O重合）运动至何处时，线段OE的长有最大值，求出这个最大值；

（3）是否存在这样的点P，使△PED是等腰三角形？若存在，请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积；若不存在，请说明理由．

Answer 1

【答案】（1），B（1，0）；（2）；（3）点P的坐标为（4，0）时，此 时△PED与正方形ABCD重叠部分的面积为．

【解析】分析：（1）将点A的坐标代入二次函数的解析式求得其解析式，然后求得点B的坐标即可求得正方形ABCD的边长，从而求得点D的纵坐标.

（2）PA=t，OE=l，利用△DAP∽△POE得到比例式，从而得到有关两个变量的二次函数，求最值即可.

（3）分点P位于y轴左侧和右侧两种情况讨论即可得到重叠部分的面积.

详解：（1）将点A（﹣3，0）代入y=x2+bx﹣得﹣3b﹣=0，解得b=1，

∴二次函数的表达式为y=x2+x﹣，

当y=0时， x2+x﹣=0，解得x1=1，x2=﹣3，

∴B（1，0）；

（2）设PA=t（﹣3＜t＜0），则OP=3﹣t，如图1，

∵DP⊥PE，

∴∠DPA=∠PEO，

∴△DAP∽△POE，

∴=，即=，

∴OE=﹣t2+t

=﹣（t﹣）2+，

∴当t=时，OE有最大值，即P为AO中点时，OE的最大值为；

（3）存在．

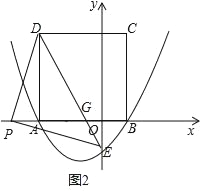
当点P在y轴左侧时，如图2，DE交AB于G点，

∵PD=PE，∠DPE=90°，

∴△DAP≌△POE，

∴PO=AD=4，

∴PA=1，OE=1，

∵AD∥OE，

∴==4，

∴AG=，

∴S△DAG=4=，

∴P点坐标为（﹣4，0），此时△PED与正方形ABCD重叠部分的面积为；

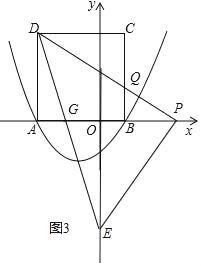
当P点在y轴右侧时，如图3，DE交AB于G点，DP与BC相交于Q，

同理可得△DAP≌△POE，

∴PO=AD=4，

∴PA=7，OE=7，

∵AD∥OE，

∴==，

∴OG=，

同理可得BQ=

∴S四边形DGBQ=×（+1）×4+×4×=

∴当点P的坐标为（4，0）时，此时△PED与正方形ABCD重叠部分的面积为．