题目内容
【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.
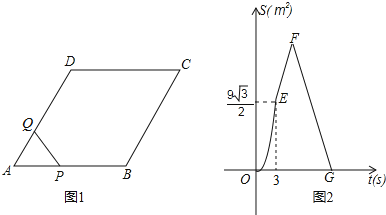
(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
【答案】(1)点Q运动的速度是1cm/s;(2)![]() ;(3)存在,t=
;(3)存在,t=![]() 或t=
或t=![]() .
.
【解析】
试题分析:(1)根据函数图象中E点所代表的实际意义求解.E点表示点P运动到与点B重合时的情形,运动时间为3s,可得AB=6cm;再由S△APQ=![]() ,可求得AQ的长度,进而得到点Q的运动速度;
,可求得AQ的长度,进而得到点Q的运动速度;
(2)函数图象中线段FG,表示点Q运动至终点D之后停止运动,而点P在线段CD上继续运动的情形.如答图2所示,求出S的表达式,并确定t的取值范围;
(3)当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,如答图3所示,求出t的值;当点P在BC上运动时,PQ将菱形分为梯形ABPQ和梯形PCDQ两部分,如答图4所示,求出t的值.
试题解析:(1)由题意,可知题图2中点E表示点P运动至点B时的情形,所用时间为3s,则菱形的边长AB=2×3=6cm.此时如答图1所示:
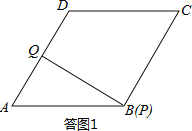
AQ边上的高h=ABsin60°=6×![]() =
=![]() cm, S=S△APQ=
cm, S=S△APQ=![]() AQh=
AQh=![]() AQ×3
AQ×3![]() =
=![]() ,解得AQ=3cm. ∴点Q的运动速度为:3÷3=1cm/s.(2)由题意,可知题图2中FG段表示点P在线段CD上运动时的情形.如答图2所示:
,解得AQ=3cm. ∴点Q的运动速度为:3÷3=1cm/s.(2)由题意,可知题图2中FG段表示点P在线段CD上运动时的情形.如答图2所示:
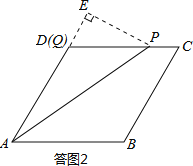
点Q运动至点D所需时间为:6÷1=6s,点P运动至点C所需时间为12÷2=6s,至终点D所需时间为18÷2=9s.
因此在FG段内,点Q运动至点D停止运动,点P在线段CD上继续运动,且时间t的取值范围为:6≤t≤9.过点P作PE⊥AD交AD的延长线于点E,则PE=PDsin60°=(18-2t)×![]() ,
,
S=S△APQ=![]() ADPE=
ADPE=![]() ×6×(
×6×(![]() +
+![]() )=
)=![]() .
.
∴FG段的函数表达式为:S=![]() (6≤t≤9).
(6≤t≤9).
(3)菱形ABCD的面积为:6×6×sin60°=18![]() ,
,
当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,如答图3所示.
此时△APQ的面积S=![]() AQAPsin60°=
AQAPsin60°=![]() t2t×
t2t×![]() =
=![]() ,
,
根据题意,得![]() =
=![]() ,
,
解得:t=![]() s,
s,

当点P在BC上运动时,PQ将菱形分为梯形ABPQ和梯形PCDQ两部分,如答图4所示.
此时,有S梯形ABPQ=![]() S菱形ABCD,即
S菱形ABCD,即![]() (2t-6+t)×6×
(2t-6+t)×6×![]() =
=![]() ×18
×18![]() ,
,
解得t=![]() s,
s,
答:存在,当t=![]() 或
或![]() 时,使PQ将菱形ABCD的面积恰好分成1:5的两部分.
时,使PQ将菱形ABCD的面积恰好分成1:5的两部分.