题目内容
【题目】已知a,b,c为正数,满足如下两个条件:a+b+c=32 ①![]() ② 是否存在以
② 是否存在以 ![]() 为三边长的三角形?如果存在,求出三角形的最大内角.
为三边长的三角形?如果存在,求出三角形的最大内角.
【答案】以 ![]() ,
,![]() ,
,![]() 为三边长可构成一个直角三角形,它的最大内角为90°
为三边长可构成一个直角三角形,它的最大内角为90°
【解析】试题分析:两个方程,有三个未知量,不能解出具体数值,但是能求出a,b,c关系,本题利用代入,因式分解,求出a,b,c关系.
试题解析:
解法1:将①②两式相乘,得![]() .
.
即: ![]() =0,
=0,
即 ![]() =0,
=0,
![]() =0,
=0,
即 ![]() ,
,
即 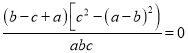 ,
,
即 ![]() ,
,
所以b﹣c+a=0或c+a﹣b=0或c﹣a+b=0,
即b+a=c或c+a=b或c+b=a .
因此,以![]() ,
, ![]() ,
, ![]() 为三边长可构成一个直角三角形,它的最大内角为90°.
为三边长可构成一个直角三角形,它的最大内角为90°.
解法2:结合①式,由②式可得得 1024-2(a2+b2+c2)= ![]() ,
,
又由①式得(a+b+c)2=1024,即a2+b2+c2=1024﹣2(ab+bc+ca),
代入③式,得 1024-2[1024-2(ab+bc+ca)]= ![]() ,
,
即abc=16(ab+bc+ca)﹣4096.
(a﹣16)(b﹣16)(c﹣16)=abc﹣16(ab+bc+ca)+256(a+b+c)﹣163=﹣4096+256×32﹣163=0,
所以a=16或b=16或c=16.
结合①式可得b+a=c或c+a=b或c+b=a .
因此,以 ![]() ,
, ![]() ,
, ![]() 为三边长可构成一个直角三角形,它的最大内角为90°.
为三边长可构成一个直角三角形,它的最大内角为90°.

练习册系列答案
相关题目




