题目内容
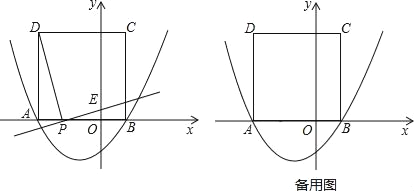
【题目】如图1,矩形ABCD的边AD在y轴上,抛物线![]() 经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上。
经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上。
(1)请直接写出下列各点的坐标:
A ,B ,C ,D ;
(2)若点P是抛物线上一动点(点P不与点A、点B重合),过点P作![]() 轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2。
轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2。
①当线段PH=2GH时,求点P的坐标;
②当点P在直线BD下方时,点K在直线BD上,且满足△KPH∽△AEF,求△KPH面积的最大值。
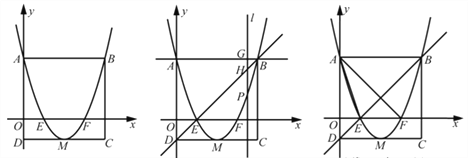
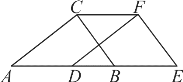
图1 图2 备用图
【答案】(1)A(0,3),B(4,3),C(4,-1),D( 0,- 1):(2)①当点P的坐标为(3,0)或(-1,8);
②![]()
【解析】试题分析:(1)令x=0,得到点A的坐标,再根据点A的纵坐标得到点B的坐标,根据抛物线的顶点式和矩形的性质可得C.D的坐标;
(2)①根据待定系数法可得直线BD的解析式,设点P的坐标为(x,x2﹣4x+3),则点H(x,x﹣1),点G(x,3).分三种情况:1°当x≥1且x≠4时;2°当0<x<1时;3°当x<0时;三种情况讨论可得点P的坐标;
②根据相似三角形的性质可得![]() ,再根据二次函数的增减性可得△KPH面积的最大值.
,再根据二次函数的增减性可得△KPH面积的最大值.
试题解析:解:(1)A(0,3),B(4,3),C(4,﹣1),D(0,﹣1).
(2)①设直线BD的解析式为y=kx+b(k≠0),由于直线BD经过D(0,﹣1),B(4,3),∴![]() ,解得:
,解得: ![]() ,∴直线BD的解析式为y=x﹣1.
,∴直线BD的解析式为y=x﹣1.
设点P的坐标为(x,x2﹣4x+3),则点H(x,x﹣1),点G(x,3).
1°当x≥1且x≠4时,点G在PH的延长线上,如图①.
∵PH=2GH,∴(x﹣1)﹣(x2﹣4x+3)=2[3﹣(x﹣1)],∴x2﹣7x+12=0,解得x1=3,x2=4.
当x2=4时,点P,H,G重合于点B,舍去,∴x=3,∴此时点P的坐标为(3,0).

2°当0<x<1时,点G在PH的反向延长线上,如图②,PH=2GH不成立.
3°当x<0时,点G在线段PH上,如图③.
∵PH=2GH,∴(x2﹣4x+3)﹣(x﹣1)=2[3﹣(x﹣1)],∴x2﹣3x﹣4=0,解得x1=﹣1,x2=4(舍去),∴x=﹣1.此时点P的坐标为(﹣1,8).
综上所述可知,点P的坐标为(3,0)或(﹣1,8).
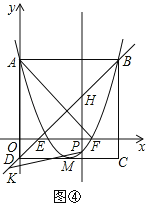
②如图④,令x2﹣4x+3=0,得x1=1,x2=3,∴E(1,0),F(3,0),∴EF=2,∴S△AEF=![]() EFOA=3.
EFOA=3.
∵△KPH∽△AEF,∴![]() ,∴
,∴![]() .
.
∵1<x<4,∴当![]() 时,s△KPH的最大值为
时,s△KPH的最大值为![]() .
.

 培优三好生系列答案
培优三好生系列答案