题目内容
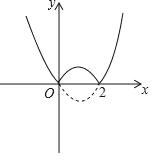
【题目】如图中实线所示,函数y=|a(x﹣1)2﹣1|的图象经过原点,小明同学研究得出下面结论:
①a=1;②若函数y随x的增大而减小,则x的取值范围一定是x<0;
③若方程|a(x﹣1)2﹣1|=k有两个实数解,则k的取值范围是k>1;
④若M(m1,n),N(m2,n),P(m3,n),Q(m4,n)(n>0)是上述函数图象的四个不同点,且m1<m2<m3<m4,则有m2+m3﹣m1=m4.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】C
【解析】
①根据函数图像经过原点![]() ,可得
,可得![]() ;②由函数的图像可知:顶点坐标(1,1),与x轴的交点坐标(0,0),(2,0),当
;②由函数的图像可知:顶点坐标(1,1),与x轴的交点坐标(0,0),(2,0),当![]() 或
或![]() 时,函数y随x的增大而减小;③若方程
时,函数y随x的增大而减小;③若方程![]() 有两个实数解,
有两个实数解,![]() 或
或![]() ;④由函数的图像可知,直线
;④由函数的图像可知,直线![]() )与函数
)与函数![]() 的图像有四个交点,由m1<m2<m3<m4
的图像有四个交点,由m1<m2<m3<m4
可知![]() ,移项可得
,移项可得![]() .
.
解:(1)∵函数![]() 图像经过原点,
图像经过原点,
∴![]() ,
,
解得:![]() ,故①正确;
,故①正确;
(2)由函数图像可知顶点坐标(1,1),与x轴的交点坐标(0,0),(2,0),
∵函数y随x的增大而减小,
∴![]() 或
或![]() ,故②错误;
,故②错误;
(3)∵方程![]() 有两个实数解,
有两个实数解,
∴![]() 或
或![]() ,故③错误;
,故③错误;
(4)∵M(m1,n),N(m2,n),P(m3,n),Q(m4,n)(n>0)是上述函数图象的四个不同点,
∴直线![]() 自变量取值范围为
自变量取值范围为![]() )
)
∴m1与m4,m2与m3关于x=1对称,
∴![]() ,即
,即![]() ,
,
故④正确;
故答案为:C.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目