题目内容
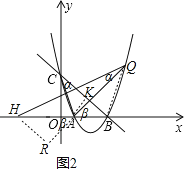
【题目】如图,在平面直角坐标系中,直线y=﹣x+5与x轴交于点B,与y轴交于点C.抛物线y=x2+bx+c经过点B和点C,与x轴交于另一点A,连接AC.
(1)求抛物线的解析式;
(2)若点Q在直线BC上方的抛物线上,连接QC,QB,当△ABC与△QBC的面积比等于2:3时,直接写出点Q的坐标:
(3)在(2)的条件下,点H在x轴的负半轴,连接AQ,QH,当∠AQH=∠ACB时,直接写出点H的坐标.
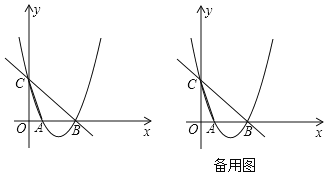
【答案】(1)y=x2﹣6x+5;(2)点Q(﹣1,12)或(6,5);(3)点H的坐标为:(﹣19,0)或(﹣![]() ,0).
,0).
【解析】
(1)直线y=-x+5与x轴交于点B,与y轴交于点C,则点B、C的坐标分别为:(5,0)、(0,5),即可求解;
(2)过点A作直线BC的平行线n交y轴于点M,则点M(0,1),则CM=5-1=4,在点C上方取CN=![]() CM=6,过点N作直线m交抛物线于点Q(Q′),则点Q为所求,即可求解
CM=6,过点N作直线m交抛物线于点Q(Q′),则点Q为所求,即可求解
(3)分点Q(6,5)、点Q(-1,12)两种情况,分别求解即可.
解:(1)直线y=﹣x+5与x轴交于点B,与y轴交于点C,则点B、C的坐标分别为:(5,0)、(0,5),则c=5,将点B的坐标代入抛物线表达式并解得:b=﹣6,
故抛物线的表达式为:y=x2﹣6x+5;
(2)过点A作直线BC的平行线n交y轴于点M,则点M(0,1),则CM=5﹣1=4,
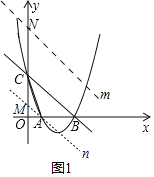
在点C上方取CN=![]() CM=6,过点N作直线m交抛物线于点Q(Q′),则点Q为所求,
CM=6,过点N作直线m交抛物线于点Q(Q′),则点Q为所求,
则点N(0,11),则直线m的表达式为:y=﹣x+11…②,
联立①②并解得:x=﹣1或6,
故点Q(﹣1,12)或(6,5);
(3)过点A作AK⊥BC于点K,
AB=4,则AK=BK=![]() ,AC=
,AC=![]() ,
,
则sin∠ABC=![]() =sinα,则tanα=
=sinα,则tanα=![]() ;
;
①当点Q(6,5)时,
过点H作HR⊥AQ交QA的延长线于点R
由点A、Q的坐标知,tan∠QAB=1=tanβ,故β=45°,AQ=5![]() ,
,
则HR=AR=x,tan∠HQR=tanα=![]() ,
,
解得:x=10![]() ,AH=
,AH=![]() x=20,
x=20,
故点H(﹣19,0);
②当点Q(﹣1,12)时,
同理可得:点H(﹣![]() ,0);
,0);
综上,点H的坐标为:(﹣19,0)或(﹣![]() ,0).
,0).