Question

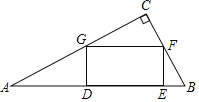
【题目】如图，在△ABC中，∠C＝90°，矩形DEFG的顶点G、F分别在AC、BC上，DE在AB上，设AG＝5，AD＝4，求△ADG与△FEB的面积比．

Answer 1

【答案】16：9．

【解析】

通过两个角对应相等可证明△ADG∽△FEB，再根据勾股定理和相似三角形的性质解答即可．

解：∵∠C＝90°，

∴∠A+∠B＝90°，

∵四边形DEFG是矩形，

∴∠GDE＝∠FED＝90°，

∴∠GDA+∠FEB＝90°，

∴∠A+∠AGD＝90°，

∴∠B＝∠AGD，

且∠GDA＝∠FEB＝90°，

∴△ADG∽△FEB．

在Rt△AGD中，∠GDA＝90°，

由勾股定理得，AD2+GD2＝AG2，

∵AD＝4，AG＝5，

∴GD＝3，

∴EF＝3，

∴，

∴△ADG与△FEB的面积比是16：9．