题目内容
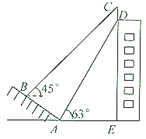
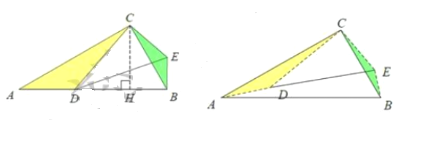
【题目】将大小两把含30°角的直角三角尺按如图1 位置摆放,即大小直角三角尺的直角顶点C 重合,小三角尺的顶点 D、E 分别在大三角尺的直角边 AC、BC 上,此时小三角尺的斜边 DE 恰好经过大三角尺的重心G .已知A CDE 30°, AB 12 .
(1)求小三角尺的直角边CD 的长;
(2)将小三角尺绕点C 逆时针旋转,当点D第一次落在大三角尺的边 AB 上时(如图2),求点 B 、 E 之间的距离;
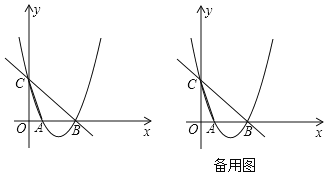
(3)在小三角尺绕点C 旋转的过程中,当直线 DE 经过点 A 时,求BAE 的正弦值.

【答案】(1)CD=4![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)求出BC,AC,利用重心即可解答.
(2) 做CH⊥AB于H,根据条件求出AD,利用三角形相似即可解答.
(3)分类讨论DE在AC下方和DE在AC上方时的情况,利用勾股定理即可解答.
解:(1)根据题意得BC=6,AC=6![]() ,
,
由重心性质可得![]() ,
,
可得CD=4![]() .
.
(2)做CH⊥AB于H,
可得BH=3,CH=3![]() ,AH=9,
,AH=9,
∵CD=4![]() ,即DH=
,即DH=![]() =
=![]() .
.
∴AD=9-![]() .
.
∵∠ACD=∠BCE,![]() ,
,
所以△ACD∽△BCE,
所以![]() ,即BE=3
,即BE=3![]() -
-![]() .
.
(3)①DE在AC下方时:△ACD∽△BCE,
得∠BED=∠ADC=∠DCE+∠CED,![]() ,
,
∴∠AEB=∠DCE=90°,设BE=x,AD=![]() x,
x,
在Rt△ABE中,![]() ,
,
可得x=4![]() -2
-2![]() .
.
所以sin∠BAE=![]() =
=![]() .
.
②DE在AC上方时,
同理![]() ,
,
∠BEC+∠DEC=∠D+∠DEC=90°,
∴∠AEB=90,
设BE=x,AD=![]() x,AE=
x,AE=![]() x-8,
x-8,
在直角三角形ABE中,![]() ,
,
解得x=4![]() +2
+2![]() ,
,
所以sin∠BAE=![]() .
.
故BAE 的正弦值.为![]() 或
或![]() .
.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
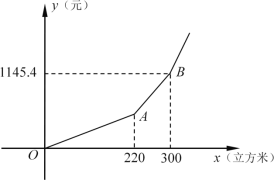
天天练口算系列答案【题目】上海市为了增强居民的节水意识,避免水资源的浪费,全面实施居民“阶梯水价”.当累计水量达到年度阶梯水量分档基数临界点后,即开始实施阶梯价格计价,分档水量和价格见下表.
分档 | 户年用水量 (立方米) | 自来水价格 (元/立方米) | 污水处理费 (元/立方米) |
第一阶梯 | 0-220(含220) | 1.92 | 1.70 |
第二阶梯 | 220-300(含300) | 3.30 | 1.70 |
第三阶梯 | 300以上 | 4.30 | 1.70 |
注:1.应缴纳水费 = 自来水费总额 + 污水处理费总额 2.应缴纳污水处理费总额 = 用水量×污水处理费× 0.9 | |||
仔细阅读上述材料,请解答下面的问题,并把答案写在答题纸上:
(1)小静家2019年上半年共计用水量100立方米,应缴纳水费 元;
(2)小静家全年缴纳的水费共计1000.5元,那么2019年全年用水量为 立方米;
(3)如图所示是上海市“阶梯水价”y与用水量x的函数关系,那么第二阶梯(线段AB)的函数解析式为 ,定义域 .