Question

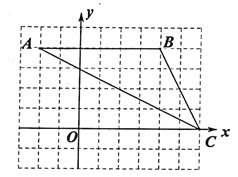
【题目】如图1，在矩形中，，，是边上一点，连接，将矩形沿折叠，顶点恰好落在边上点处，延长交的延长线于点．

（1）求线段的长；

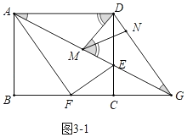
（2）如图2，，分别是线段，上的动点（与端点不重合），且．

①求证：∽；

②是否存在这样的点，使是等腰三角形？若存在，请求出的长；若不存在，请说明理由．

Answer 1

【答案】（1）3；（2）①见解析；②存在．由①得△DMN∽△DGM，理由见解析

【解析】

（1）根据矩形的性质和折叠的性质得出AD=AF、DE=EF，进而设EC＝x，则DE＝EF＝8﹣x，利用勾股定理求解即可得出答案；

（2）①根据平行线的性质得出△DAE∽△CGE求得CG＝6，进而根据勾股定理求出DG=10，得出AD=DG，即可得出答案；②假设存在，由①可得当△DGM是等腰三角形时△DMN是等腰三角形，分两种情况进行讨论：当MG＝DG=10时，结合勾股定理进行求解；当MG＝DM时，作MH⊥DG于H，证出△GHM∽△GBA，即可得出答案.

解：（1）如图1中，∵四边形ABCD是矩形，

∴AD＝BC＝10，AB＝CD＝8，∠B＝∠BCD =∠D＝90°，

由翻折可知：AD＝AF＝10．DE＝EF，设EC＝x，则DE＝EF＝8﹣x．

在Rt△ABF中，BF＝＝6，

∴CF＝BC﹣BF＝10﹣6＝4，

在Rt△EFC中，则有：（8﹣x）2＝x2+42，

∴x＝3，

∴EC＝3．

（2）①如图2中，

∵AD∥CG，

∴∠DAE=∠CGE，∠ADE=∠GCE

∴△DAE∽△CGE

∴＝，

∴，

∴CG＝6，

∴在Rt△DCG中，，

∴AD=DG

∴∠DAG＝∠AGD，

∵∠DMN＝∠DAM

∴∠DMN＝∠DGM

∵∠MDN=∠GDM

∴△DMN∽△DGM

②存在．由①得△DMN∽△DGM

∴当△DGM是等腰三角形时△DMN是等腰三角形

有两种情形：

如图3﹣1中，当MG＝DG=10时，

∵BG＝BC+CG＝16，

∴在Rt△ABG中，，

∴AM＝AG - MG = ．

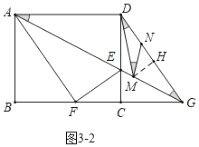
如图3﹣2中，当MG＝DM时，作MH⊥DG于H．

∴DH＝GH＝5，

由①得∠DGM =∠DAG=∠AGB

∵∠MHG =∠B

∴△GHM∽△GBA

∴，

∴，

∴，

∴．

综上所述，AM的长为或．