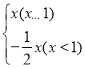Question

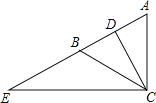
【题目】如图，在△ABC中，AB=AC，CD是AB边上的中线，延长AB到点E，使BE=AB，连接CE．求证：CD= CE．

Answer 1

【答案】见解析

【解析】

试题作BF∥AC交EC于F，通过证明△FBC≌△DBC，得到CD=CF，根据三角形中位线定理得到CF=CE，等量代换得到答案．

试题解析：证明：作BF∥AC交EC于F．

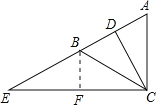
∵BF∥AC，∴∠FBC=∠ACB．∵AB=AC，∴∠ABC=∠ACB，∴∠FBC=∠ABC．

∵BF∥AC，BE=AB，∴BF= AC，CF=CE．

∵CD是AB边上的中线，∴BD=AB，∴BF=BD．

在△FBC和△DBC中，∵BF＝BD，∠FBC＝∠DBC，BC＝BC，∴△FBC≌△DBC，∴CD=CF，∴CD=CE．