Question

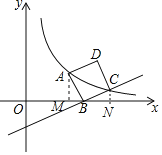
【题目】如图，正方形ABCD的顶点B在x轴上，点A、点C在双曲线y＝（k＞0，x＞0）上．若直线BC的解析式为y＝x﹣2，则k的值为（　　）

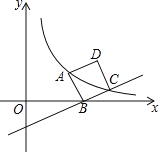
A.24B.12C.6D.4

Answer 1

【答案】C

【解析】

过点A、B作AM⊥x轴于M，BN⊥x轴于N，可证明△ABM≌△BNC，得到BN＝AM，BM＝CN，可证明△BOE∽△BNC，得到BN＝2CN，设C(4+2a，a)，则B(4﹣a，2a)，得到k＝(4+2a)a＝(4﹣a)2a，求得a的值，得到C的坐标，从而求得k的值．

解：分别过点A、B作AM⊥x轴于M，BN⊥x轴于N，则∠BMA＝∠CNB＝90°，

∵正方形ABCD，

∴∠ABC＝90°，AB＝BC，

∴∠MBA+∠BAM＝90°，∠MBA+∠CBN＝90°，

∴∠BAM＝∠CBN．

在△ABM和△BCN中，

，

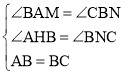∴△ABM≌△BCN（AAS），

∴BN＝AM，BM＝CN，

由直线y＝x﹣2可知B(4，0)，E(0，﹣2)，

∵∠OBE＝∠NBC，∠BOE＝∠BNC＝90°，

∴△BOE∽△BNC，

∴＝＝＝2，

∴BN＝2CN，

∴设C(4+2a，a)，则B(4﹣a，2a)，

∵A、C都在y＝（k＞0，x＞0）上，

∴k＝(4+2a)a＝(4﹣a)2a，

解得a＝1．

∴C(6，1)，

∴k＝6×1＝6，

故选：C．