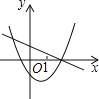题目内容
【题目】如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过B、C两点,与x轴另一交点为A,顶点为D.
(1)求抛物线的解析式;
(2)在x轴上找一点E,使△EDC的周长最小,求符合条件的E点坐标;
(3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在,求出PB2的值;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)点E(![]() ,0);(3)PB2的值为16+8
,0);(3)PB2的值为16+8![]() .
.
【解析】
(1)求出点B、C的坐标分别为(3,0)、(0,3),将点B、C的坐标代入二次函数表达式,即可求解;
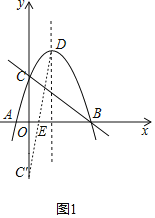
(2)如图1,作点C关于x轴的对称点C′,连接CD′交x轴于点E,则此时EC+ED为最小,△EDC的周长最小,即可求解;
(3)分点P在x轴上方、点P在x轴下方两种情况,由勾股定理可求解.
(1)直线y=﹣x+3与x轴、y轴分别交于B、C两点,
令x=0,则y=3,令y=0,则x=3,
∴点B、C的坐标分别为(3,0)、(0,3),
将点B、C的坐标代入二次函数表达式得:
![]() ,解得:
,解得:![]() ,
,
故函数的表达式为:y=﹣x2+2x+3;
(2)如图1,作点C关于x轴的对称点C′,连接CD′交x轴于点E,此时EC+ED为最小,则△EDC的周长最小,
令x=0,则﹣x2+2x+3=0,
解得:![]() ,
,
∴点A的坐标为(-1,0),
∵y=﹣x2+2x+3![]() ,
,
∴抛物线的顶点D的坐标为(1,4),则点C′的坐标为(0,﹣3),
设直线C′D的表达式为![]() ,
,
将C′、D的坐标代入得![]() ,
,
解得:![]() ,
,
∴直线C′D的表达式为:y=7x﹣3,
当y=0时,x=![]() ,
,
故点E的坐标为(![]() ,0);
,0);
(3)①当点P在x轴上方时,如图2,
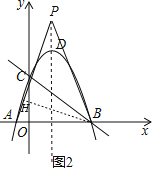
∵点B、C的坐标分别为(3,0)、(0,3),
∴OB=OC=3,则∠OCB=45°=∠APB,
过点B作BH⊥AP于点H,设PH=BH=a,
则PB=PA=![]() a,
a,
由勾股定理得:AB2=AH2+BH2,
∴16=a2+(![]() a﹣a)2,解得:a2=8+4
a﹣a)2,解得:a2=8+4![]() ,
,
则PB2=2a2=16+8![]() ;
;
②当点P在x轴下方时,
同理可得![]() .
.
综合以上可得,PB2的值为16+8![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案