题目内容
【题目】如图,在△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂线,交BC于P点,则P即为所求;
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求.
对于两人的作法,下列判断何者正确?( )
![]()
A. 两人皆正确B. 两人皆错误C. 甲正确,乙错误D. 甲错误,乙正确
【答案】C
【解析】
根据甲乙两人作图的作法:
甲:利用垂直平分线的性质得到AP=PB,得到∠PAB=∠PBA,再利用三角形的外角等于不相邻的两个内角的和,即可求出结果.
乙:根据作图的要求, AB=BP,得到∠BAP=∠APB,进一步证明即可发现∠APC≠2∠ABC,此方法不正确.
解:如图1,
由甲的作图知PQ垂直平分AB,
则PA=PB,
∴∠PAB=∠PBA,
又∠APC=∠PAB+∠PBA,
∴∠APC=2∠ABC,
故甲的作图正确;
如图2,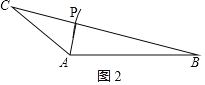
∵AB=BP,
∴∠BAP=∠APB,
∵∠APC=∠BAP+∠ABC,
∴∠APC≠2∠ABC,
∴乙错误;
故选:C.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目