题目内容
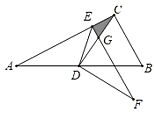
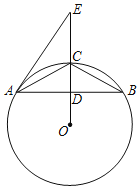
【题目】如图,⊙O为△ABC的外接圆,D为OC与AB的交点,E为线段OC延长线上一点,且∠EAC=∠ABC.
(1)求证:直线AE是⊙O的切线.
(2)若D为AB的中点,CD=6,AB=16
①求⊙O的半径;
②求△ABC的内心到点O的距离.
【答案】(1)详见解析;(2)①![]() ;②5.
;②5.
【解析】
(1)连接AO,并延长AO交⊙O于点F,连接CF,由圆周角定理可得∠ACF=90°,可得∠F+∠FAC=90°,由∠EAC=∠ABC,可得∠EAC+∠FAC=90°,即可得结论;
(2)①由垂径定理可得OD⊥AB,AD=BD=8,由勾股定理可求⊙O的半径;
②作∠CAB的平分线交CD于点H,连接BH,过点H作HM⊥AC,HN⊥BC,由角平分线的性质可得HM=HN=HD,由三角形的面积公式可求HD的值,即可求△ABC的内心到点O的距离.
解:(1)证明:连接AO,并延长AO交⊙O于点F,连接CF
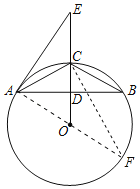
∵AF是直径
∴∠ACF=90°
∴∠F+∠FAC=90°,
∵∠F=∠ABC,∠ABC=∠EAC
∴∠EAC=∠F
∴∠EAC+∠FAC=90°
∴∠EAF=90°,且AO是半径
∴直线AE是⊙O的切线.
(2)①如图,连接AO,
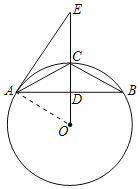
∵D为AB的中点,OD过圆心,
∴OD⊥AB,AD=BD=![]() AB=8,
AB=8,
∵AO2=AD2+DO2,
∴AO2=82+(AO﹣6)2,
∴AO=![]() ,
,
∴⊙O的半径为![]() ;
;
②如图,作∠CAB的平分线交CD于点H,连接BH,过点H作HM⊥AC,HN⊥BC,

∵OD⊥AB,AD=BD
∴AC=BC,且AD=BD
∴CD平分∠ACB,且AH平分∠CAB
∴点H是△ABC的内心,且HM⊥AC,HN⊥BC,HD⊥AB
∴MH=NH=DH
在Rt△ACD中,AC=![]() ,
,
∵S△ABC=S△ACH+S△ABH+S△BCH,
∴![]() ×16×6=
×16×6=![]() ×10×MH+
×10×MH+![]() ×16×DH+
×16×DH+![]() ×10×NH,
×10×NH,
∴DH=![]() ,
,
∵OH=CO﹣CH=CO﹣(CD﹣DH),
∴OH=![]() ﹣(6﹣
﹣(6﹣![]() )=5.
)=5.

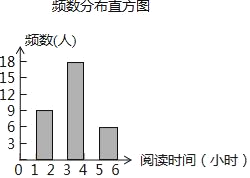
【题目】向阳中学为了解全校学生利用课外时间阅读的情况,调查者随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表(图).根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
1≤x<2 | 9 | 0.15 |
2≤x<3 | a | m |
3≤x<4 | 18 | 0.3 |
4≤x<5 | 12 | n |
5≤x<6 | 6 | 0.1 |
合计 | b | 1 |
(1)填空:a= ,b= ,m= ,n= ;
(2)将频数分布直方图补充完整;
(3)阅读时间不低于5小时的6人中,有2名男生、4名女生.现从这6名学生中选取两名同学进行读书宣讲,求选取的两名学生恰好是两名女生的概率.